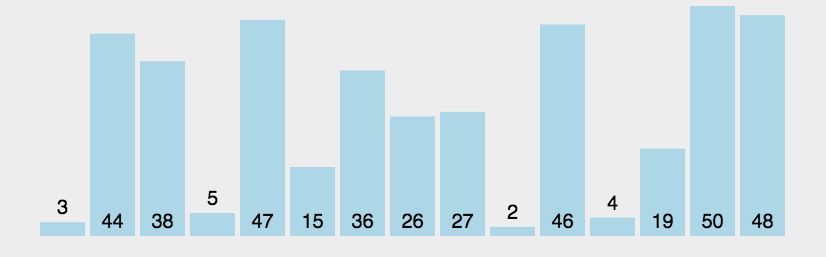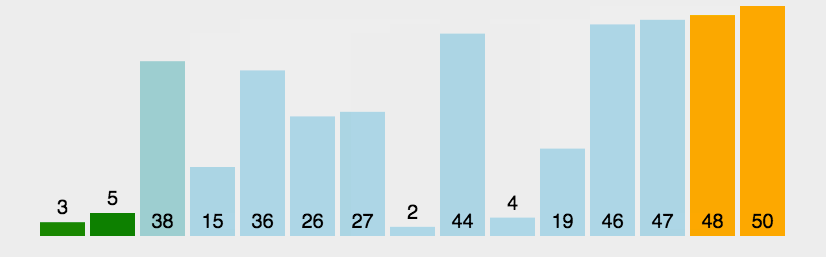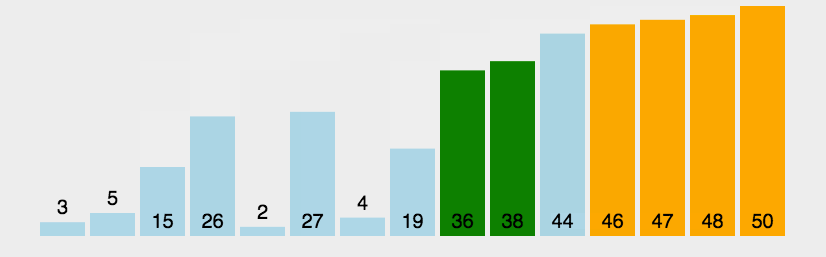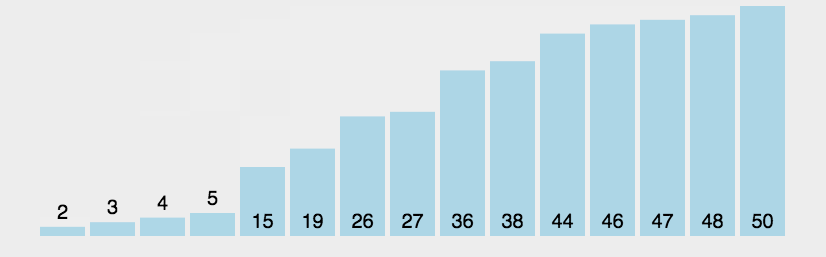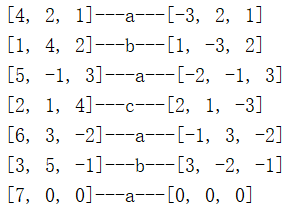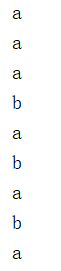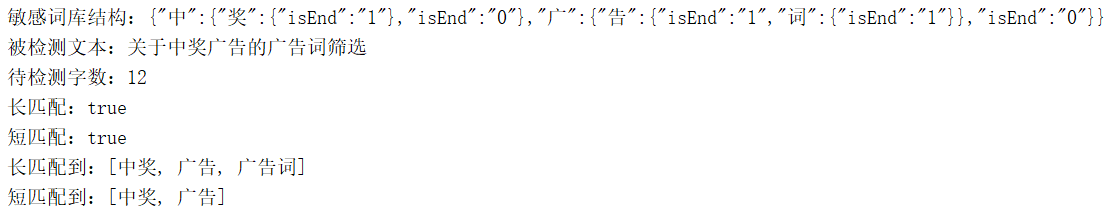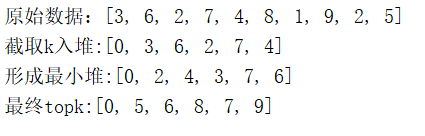数据结构 数据结构 数据结构介绍 数据结构 : 其实就是存储数据和表示数据的方式 。数据结构内容比较多,细细的学起来也是相对费功夫的,不可能达到一蹴而就。我们将常见的数据结构:堆栈、队列、数组、链表和红黑树 这几种给大家介绍一下,作为数据结构的入门,了解一下它们的特点即可。
常见数据结构 数据存储的常用结构有:栈、队列、数组、链表和红黑树。我们分别来了解一下:
栈(stack,堆栈):压栈弹栈,先进后出,子弹压膛发射。
队列(queue):先进先出,火车过山洞。
数组:查询快,增删慢。
查询[快]:连续的空间,有索引,存的是首地址,如int[],首地址0x001,后续只要首地址+索引*4个字节。
增加[慢]:长度固定不变,就得新建数组,复制,每个值地址都会改变。
删除[慢],新建数组或者后面数据整体前移,后面的数据值地址都会改变。
链表(单/双向链表):单:手拉手,查询慢,增删快。
查询[慢]:数据是离散的,必须一个一个找。
增[快]:因为链表中的要新增数据或者减少数据,只要开一个新的空间,将2个节点的地址部分数据修改一次即可,其他链表中的所有数据不用做改变。
红黑树(二叉查找平衡树):查询增删速度特别快,效率高。
二叉树:最多两个子节点的数
查询树或者排序树:二叉树的基础上,满足节点一定符合左小右大的特点。
平衡树,左右的节点相近。
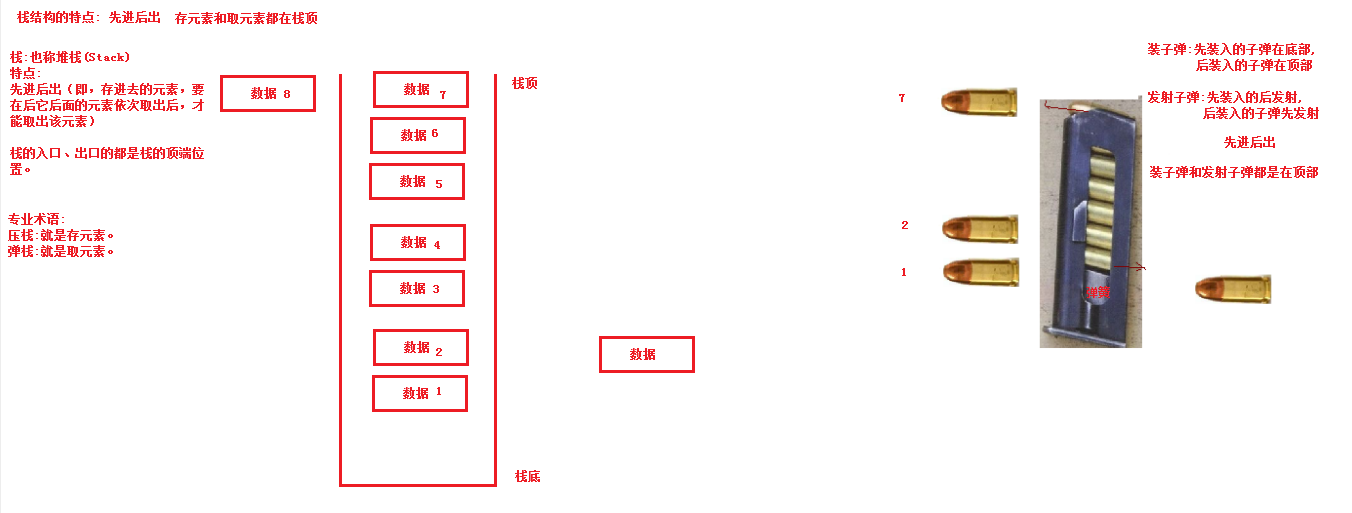
栈 栈 :stack ,又称堆栈,它是运算受限的线性表,其限制是仅允许在表的一端进行插入和删除操作,不允许在其他任何位置进行添加、查找、删除等操作。
简单的说:采用该结构的集合,对元素的存取有如下的特点
这里两个名词需要注意:
压栈 :就是存元素。即,把元素存储到栈的顶端位置,栈中已有元素依次向栈底方向移动一个位置。弹栈 :就是取元素。即,把栈的顶端位置元素取出,栈中已有元素依次向栈顶方向移动一个位置。
队列 队列 :queue ,简称队,它同堆栈一样,也是一种运算受限的线性表,其限制是仅允许在表的一端进行插入,而在表的另一端进行取出并删除。
简单的说,采用该结构的集合,对元素的存取有如下的特点:
先进先出 (即,存进去的元素,要在后它前面的元素依次取出后,才能取出该元素)。例如,小火车过山洞,车头先进去,车尾后进去;车头先出来,车尾后出来。队列的入口、出口各占一侧。 例如,下图中的左侧为入口,右侧为出口。
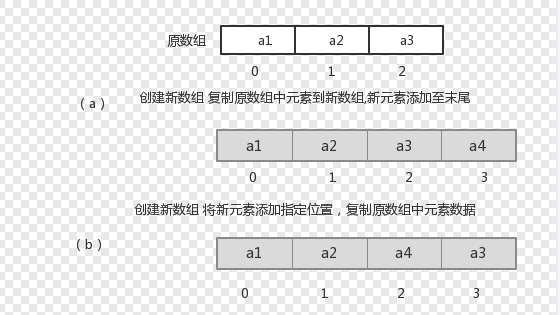
数组 数组 :Array ,是有序的元素序列,数组是在内存中开辟一段连续的空间,并在此空间存放元素。就像是一排出租屋,有100个房间,从001到100每个房间都有固定编号,通过编号 就可以快速 找到租房子的人。
简单的说,采用该结构的集合,对元素的存取有如下的特点:
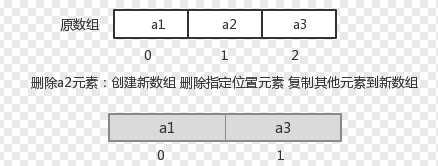
指定索引位置删除元素: 需要创建一个新数组,把原数组元素根据索引,复制到新数组对应索引的位置,原数组中指定索引位置元素不复制到新数组中。如下图
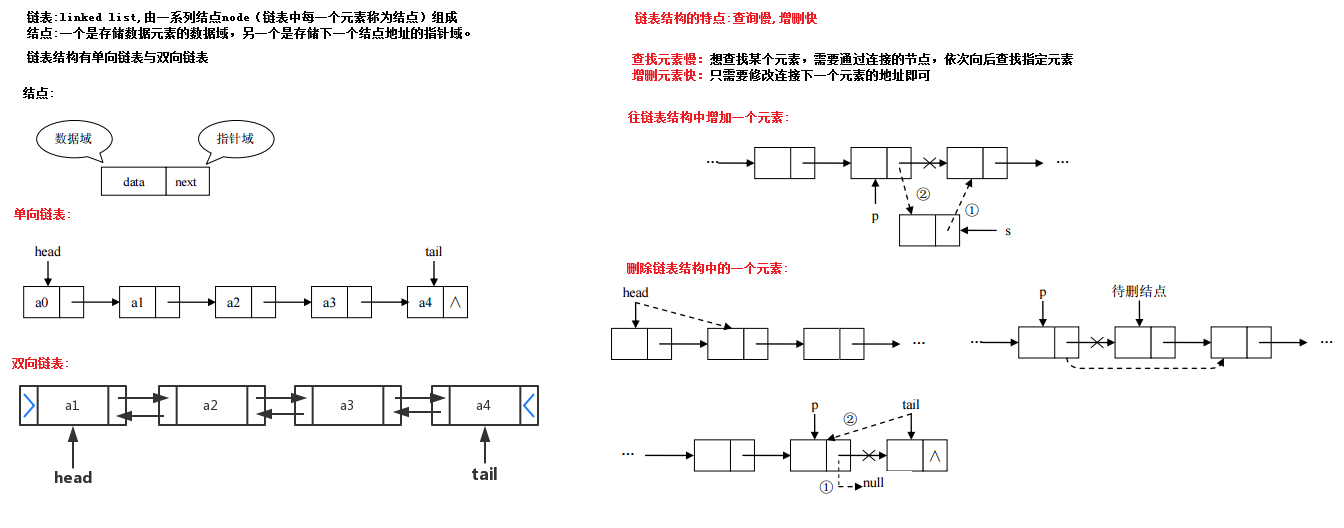
链表 链表 :linked list ,由一系列结点node(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。我们常说的链表结构有单向链表与双向链表,那么这里给大家介绍的是单向链表 。
简单的说,采用该结构的集合,对元素的存取有如下的特点:
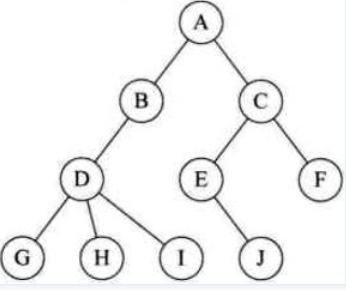
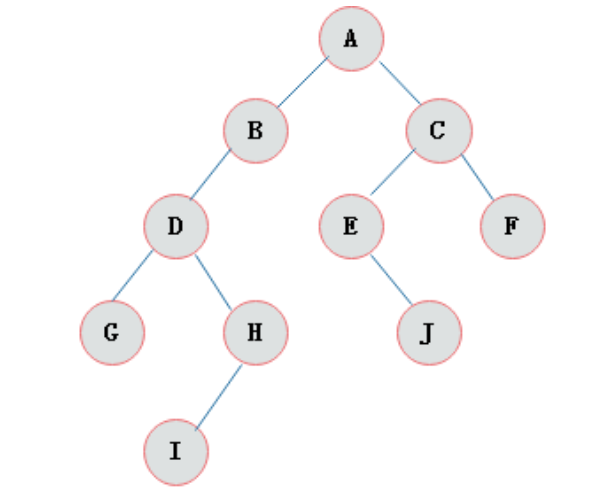
树基本结构介绍 树具有的特点
每一个节点有零个或者多个子节点
没有父节点的节点称之为根节点,一个树最多有一个根节点。
每一个非根节点有且只有一个父节点
名词
含义
节点
指树中的一个元素
节点的度
节点拥有的子树的个数,二叉树的度不大于2
叶子节点
度为0的节点,也称之为终端结点
高度
叶子结点的高度为1,叶子结点的父节点高度为2,以此类推,根节点的高度最高
层
根节点在第一层,以此类推
父节点
若一个节点含有子节点,则这个节点称之为其子节点的父节点
子节点
子节点是父节点的下一层节点
兄弟节点
拥有共同父节点的节点互称为兄弟节点
二叉树 如果树中的每个节点的子节点的个数不超过2,那么该树就是一个二叉树。
二叉查找树 二叉查找/排序/搜索树的特点:
左子树上所有的节点的值均小于等于他的根节点的值
右子树上所有的节点值均大于或者等于他的根节点的值
每一个子节点最多有两个子树
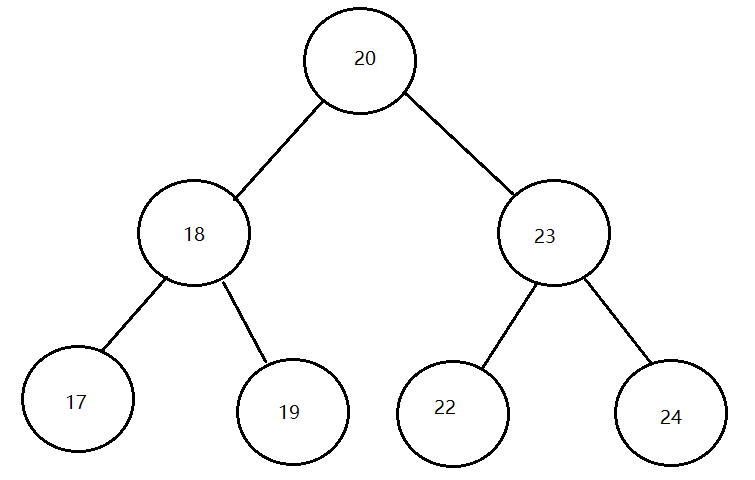
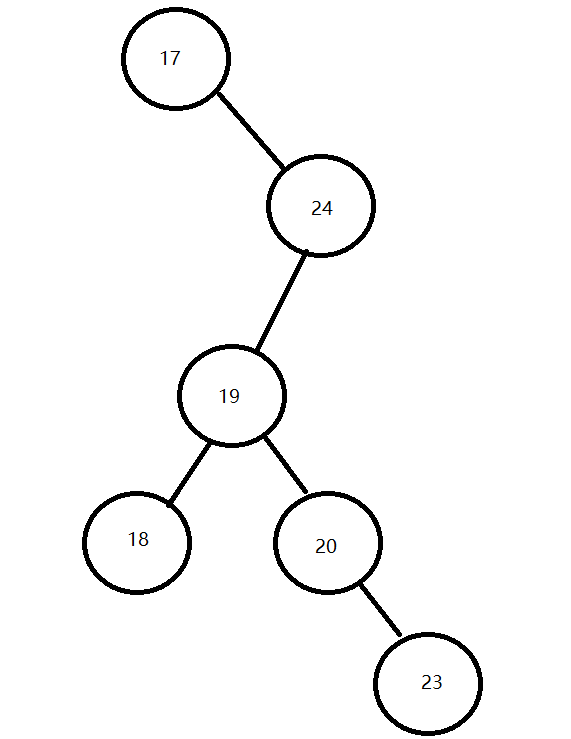
案例演示(20,18,23,22,17,24,19)数据的存储过程;
遍历获取元素的时候可以按照”左中右”的顺序进行遍历;
注意:二叉查找树存在的问题:会出现”瘸子”的现象,影响查询效率
平衡二叉树 为了避免出现”瘸子”的现象,减少树的高度,提高我们的搜素效率,又存在一种树的结构:”平衡二叉树”
规则:它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树
如下图所示:
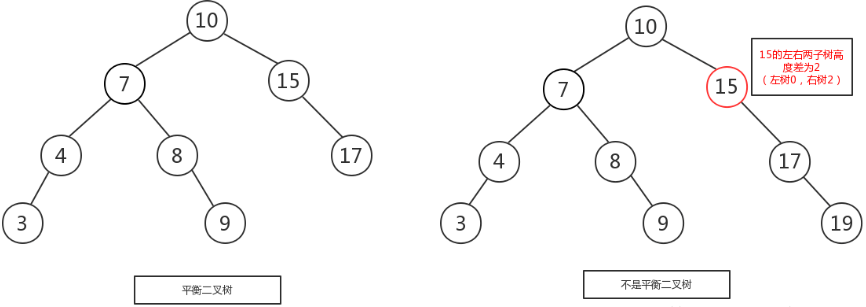
如下图所示,左图是一棵平衡二叉树,根节点10,左右两子树的高度差是1,而右图,虽然根节点左右两子树高度差是0,但是右子树15的左右子树高度差为2,不符合定义,
所以右图不是一棵平衡二叉树。
旋转 在构建一棵平衡二叉树的过程中,当有新的节点要插入时,检查是否因插入后而破坏了树的平衡,如果是,则需要做旋转去改变树的结构。
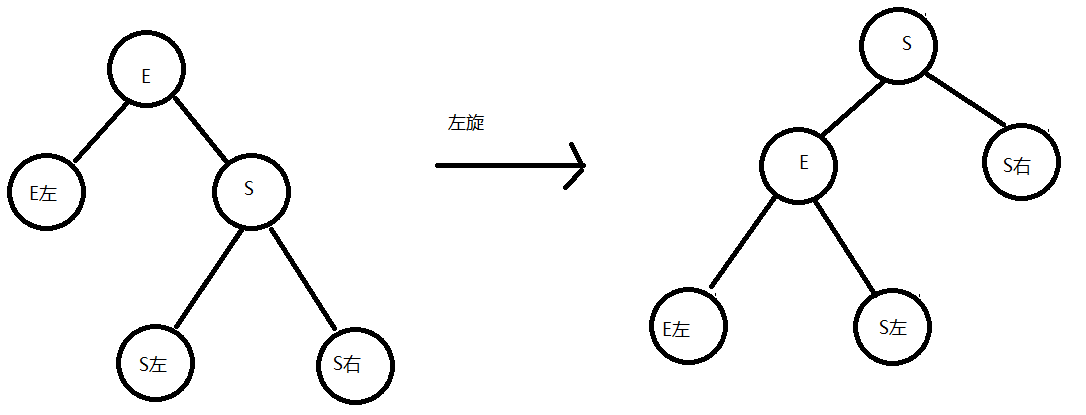
左旋 左旋就是将节点的右支往左拉,右子节点变成父节点,并把晋升之后多余的左子节点出让给降级节点的右子节点;
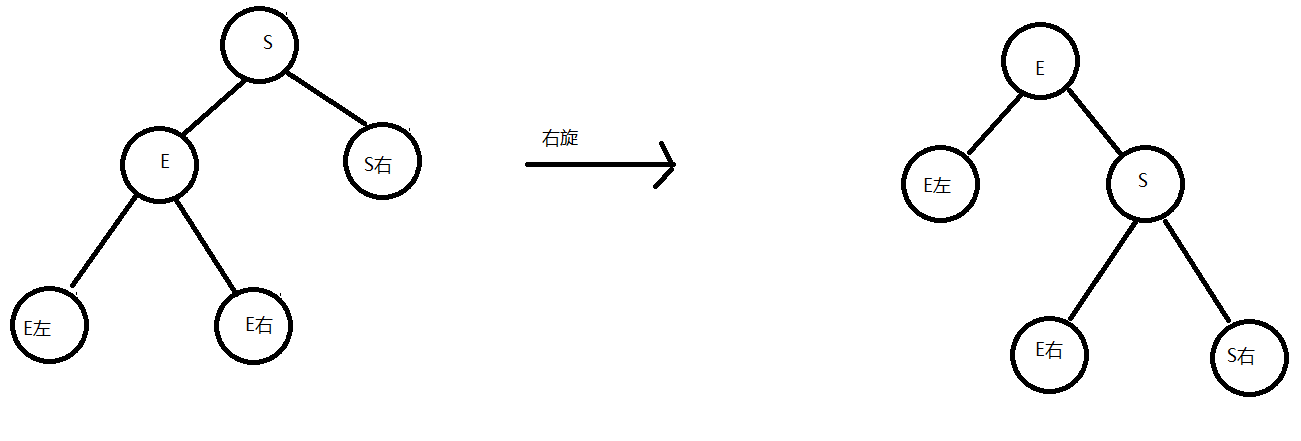
右旋 将节点的左支往右拉,左子节点变成了父节点,并把晋升之后多余的右子节点出让给降级节点的左子节点
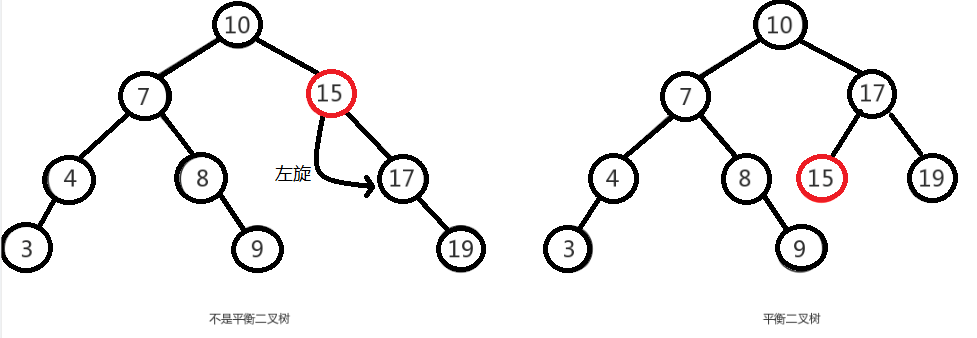
举个例子,像上图是否平衡二叉树的图里面,左图在没插入前”19”节点前,该树还是平衡二叉树,但是在插入”19”后,导致了”15”的左右子树失去了”平衡”,
所以此时可以将”15”节点进行左旋,让”15”自身把节点出让给”17”作为”17”的左树,使得”17”节点左右子树平衡,而”15”节点没有子树,左右也平衡了。如下图,
由于在构建平衡二叉树的时候,当有新节点插入 时,都会判断插入后时候平衡,这说明了插入新节点前,都是平衡的,也即高度差绝对值不会超过1。当新节点插入后,
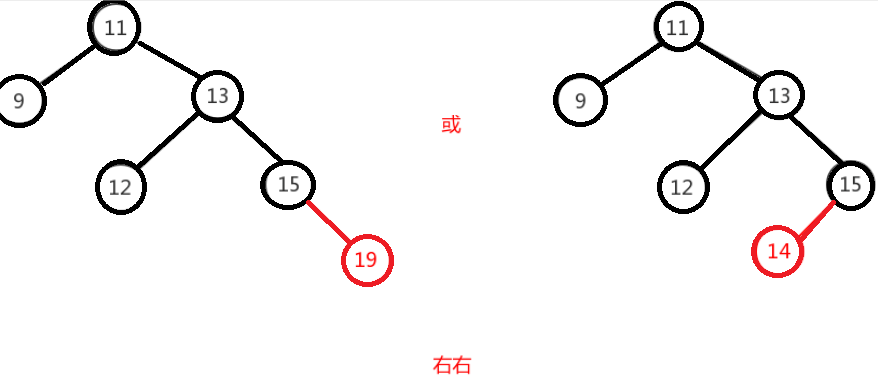
有可能会有导致树不平衡,这时候就需要进行调整,而可能出现的情况就有4种,分别称作左左,左右,右左,右右 。
1 2 3 4 5 左左:只需要做一次右旋就变成了平衡二叉树。 右右:只需要做一次左旋就变成了平衡二叉树。 左右:先做一次分支的左旋,再做一次树的右旋,才能变成平衡二叉树。 右左:先做一次分支的右旋,再做一次数的左旋,才能变成平衡二叉树。 课上只讲解“左左”的情况
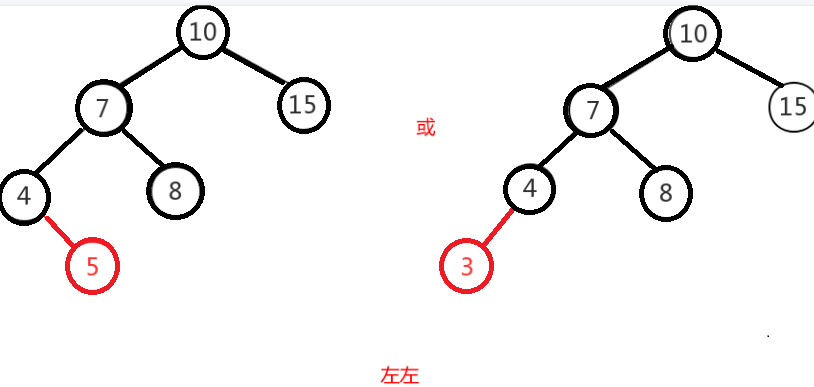
左左 左左:只需要做一次右旋就变成了平衡二叉树。
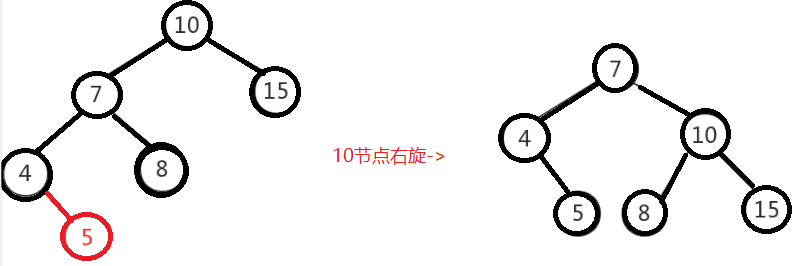
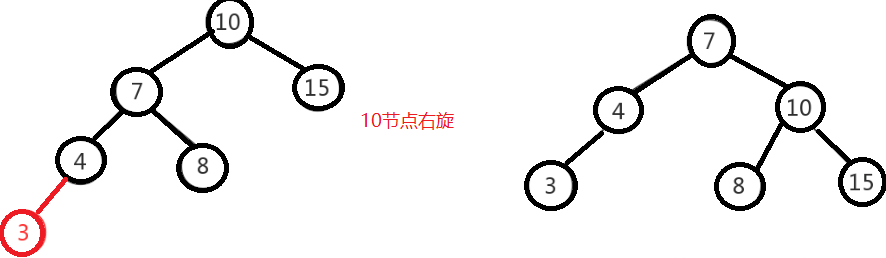
左左即为在原来平衡的二叉树上,在节点的左子树的左子树下,有新节点插入,导致节点的左右子树的高度差为2,如下即为”10”节点的左子树”7”,的左子树”4”,插入了节点”5”或”3”导致失衡。
左左调整其实比较简单,只需要对节点进行右旋即可,如下图,对节点”10”进行右旋,
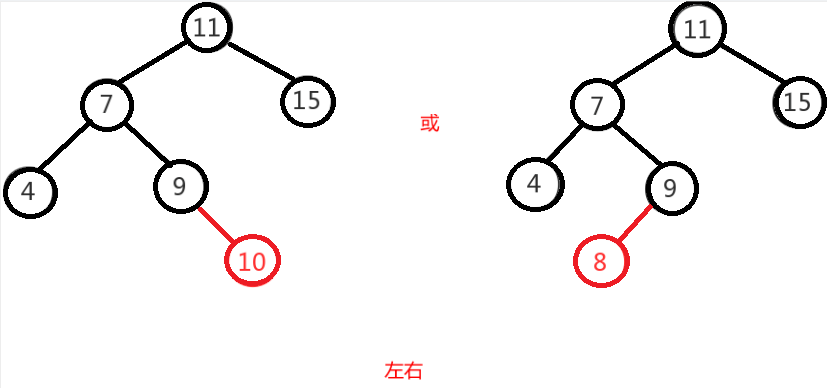
左右 左右:先做一次分支的左旋,再做一次树的右旋,才能变成平衡二叉树。
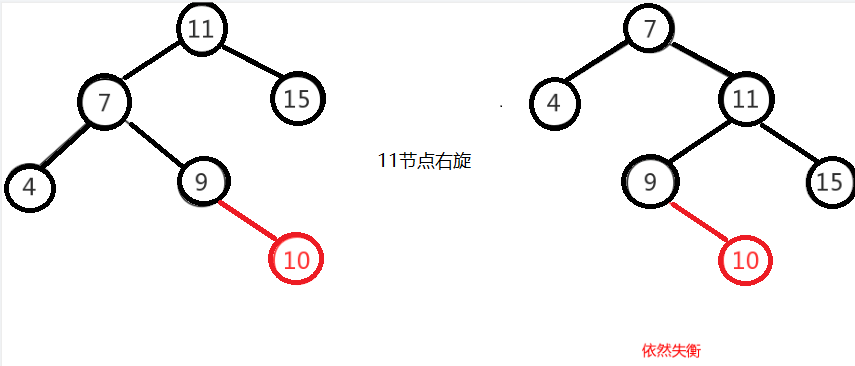
左右即为在原来平衡的二叉树上,在节点的左子树的右子树下,有新节点插入,导致节点的左右子树的高度差为2,如上即为”11”节点的左子树”7”,的右子树”9”,
插入了节点”10”或”8”导致失衡。
左右的调整就不能像左左一样,进行一次旋转就完成调整。我们不妨先试着让左右像左左一样对”11”节点进行右旋,结果图如下,右图的二叉树依然不平衡,而右图就是接下来要
讲的右左,即左右跟右左互为镜像,左左跟右右也互为镜像。
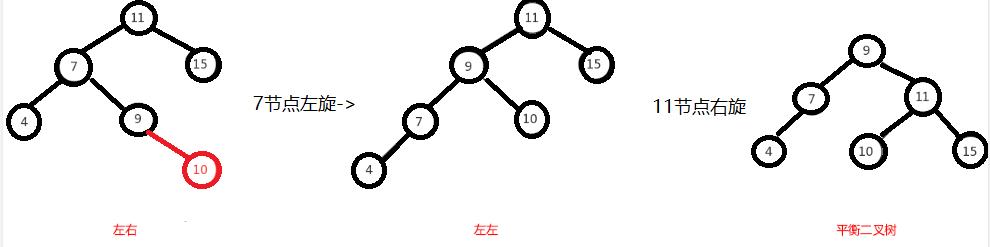
左右这种情况,进行一次旋转是不能满足我们的条件的,正确的调整方式是,将左右进行第一次旋转,将左右先调整成左左,然后再对左左进行调整,从而使得二叉树平衡。
即先对上图的节点”7”进行左旋,使得二叉树变成了左左,之后再对”11”节点进行右旋,此时二叉树就调整完成,如下图:
右左 右左:先做一次分支的右旋,再做一次数的左旋,才能变成平衡二叉树。
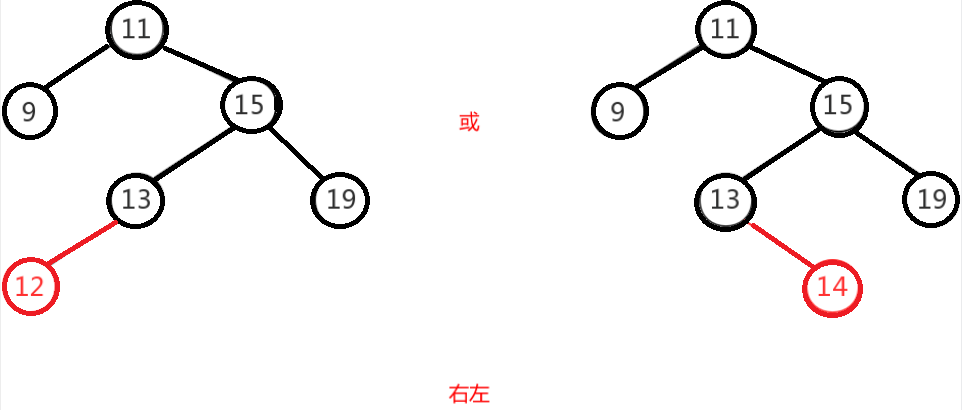
右左即为在原来平衡的二叉树上,在节点的右子树的左子树下,有新节点插入,导致节点的左右子树的高度差为2,如上即为”11”节点的右子树”15”,的左子树”13”,
插入了节点”12”或”14”导致失衡。
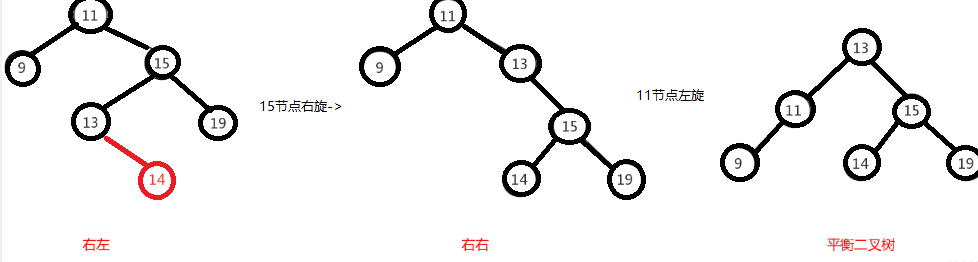
前面也说了,右左跟左右其实互为镜像,所以调整过程就反过来,先对节点”15”进行右旋,使得二叉树变成右右,之后再对”11”节点进行左旋,此时二叉树就调整完成,如下图:
右右 右右:只需要做一次左旋就变成了平衡二叉树。
右右即为在原来平衡的二叉树上,在节点的右子树的右子树下,有新节点插入,导致节点的左右子树的高度差为2,如下即为”11”节点的右子树”13”,的左子树”15”,插入了节点
“14”或”19”导致失衡。
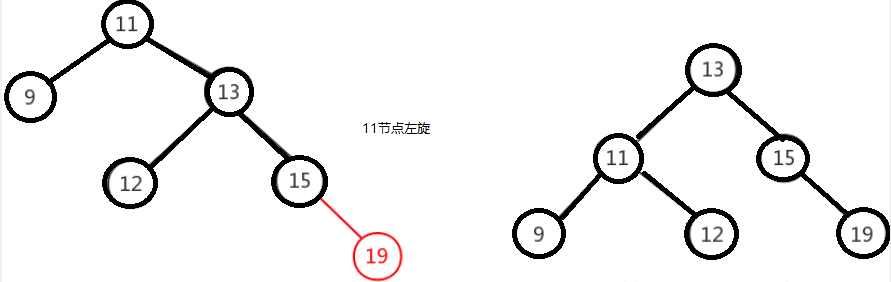
右右只需对节点进行一次左旋即可调整平衡,如下图,对”11”节点进行左旋。
红黑树 红黑树是一种自平衡的二叉查找树,是计算机科学中用到的一种数据结构,它是在1972年由Rudolf Bayer发明的,当时被称之为平衡二叉B树,后来,在1978年被
Leoj.Guibas和Robert Sedgewick修改为如今的”红黑树”。它是一种特殊的二叉查找树,红黑树的每一个节点上都有存储位表示节点的颜色,可以是红或者黑;
红黑树不是高度平衡的,它的平衡是通过”红黑树的特性”进行实现的;
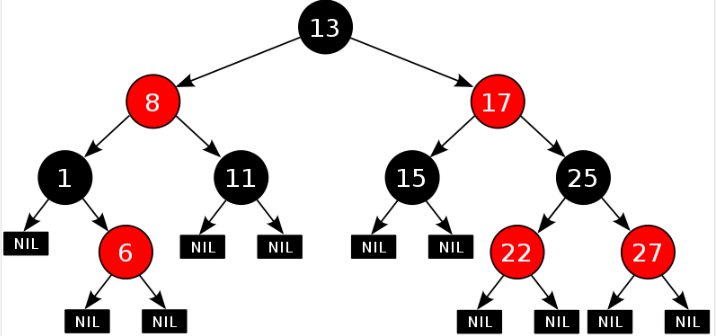
红黑树的特性:
每一个节点或是红色的,或者是黑色的。
根节点必须是黑色
每个叶节点(Nil)是黑色的;(如果一个节点没有子节点或者父节点,则该节点相应的指针属性值为Nil,这些Nil视为叶节点)
如果某一个节点是红色,那么它的子节点必须是黑色(不能出现两个红色节点相连的情况)
对每一个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点;
如下图所示就是一个
在进行元素插入的时候,和之前一样; 每一次插入完毕以后,使用黑色规则进行校验,如果不满足红黑规则,就需要通过变色,左旋和右旋来调整树,使其满足红黑规则;
小结
红黑树的作用: 提高搜索效率
表示集合的类有很多,但是每个集合存储数据的的数据结构不同,所以每个集合有各自的特点,
ArrayList集合: 查询快,增删慢 —>存储数据的数据结构是数组
LinkedList集合: 查询慢,增删快—>存储数据的数据结构是链表
…..
基础算法 为什么用排序? 通常来说,排序的目的就是快速查找
衡量排序算法的优劣
1.时间复杂度:分析关键字的比较次数和记录的移动次数
2.空间复杂度:分析排序算法中需要多少辅助内存
3.稳定性:若了两个记录A和B的关键字值相等,但排序A,B的先后次序保持不变,称为稳定的。
(关键字,更常用于对象的某个属性,比如,商品一开始按销量从高到低排了,但是有些商品的价格相同,我们再按价格从低到高排,而这时候,希望价格相同的,销量还是高的在上面。就需要一个稳定的算法。)
十大内部排序算法(内存) 外部排序(磁盘) 1.选择排序
2.交换排序
3.插入排序
直接插入排序
折半插入排序
Shell(希尔)排序
4.归并排序
5.桶式排序
6.基数排序
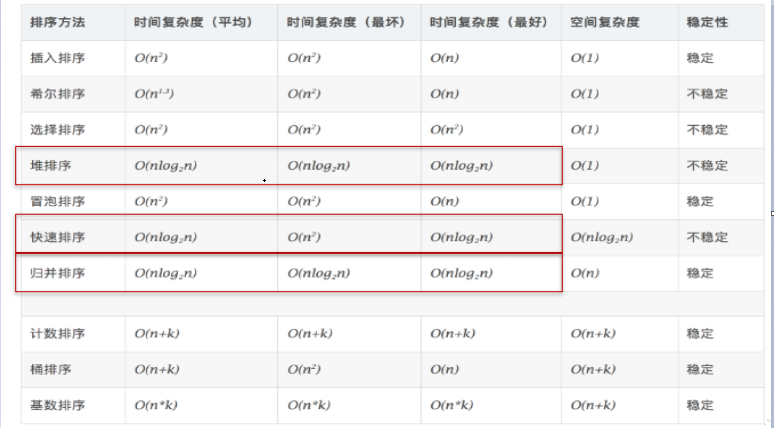
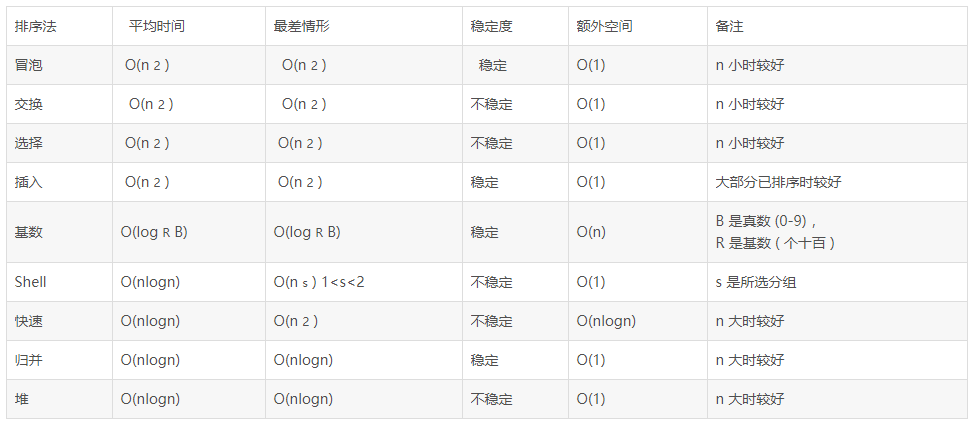
各种内部排序方法性能比较 1.从平均时间而言 :快速排序最佳 。但在最坏情况下时间性能不如堆排序和归并排序
2.从算法简单性看 :由于直接选择排序、直接插入排序和冒泡排序的算法比较简单,将其认为是简单算法。对于Shell排序、堆排序、快速排序和归并排序算法,其算法比较复杂,认为是复杂排序。
3.从稳定性看 :直接插入排序、冒泡排序和归并排序时稳定的;而直接选择排序、快速排序、 Shell排序和堆排序是不稳定排序
4.从待排序的记录数n的大小看 ,n较小时,宜采用简单排序;而n较大时宜采用改进排序
1 2 3 4 5 选择: (1 )若n较小(如n≤50 ),可采用直接插入或直接选择排序。 当记录规模较小时,直接插入排序较好;否则因为直接选择移动的记录数少于直接插入,应选直接选择排序为宜。 (2 )若文件初始状态基本有序(指正序),则应选用直接插入、冒泡或随机的快速排序为宜; (3 )若n较大,则应采用时间复杂度为O(nlgn)的排序方法:快速排序、堆排序或归并排序。
快速排序 快排概述 分治法的思想,20世纪十大算法之一,是迄今为止所有内排序算法中速度最快的一种。快速排序的时间复杂度为O(nlog(n))。
从数列中挑出一个元素,称为”基准”(pivot),
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
快排图解
代码实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 public class QuickSort { private static void swap (int [] data, int i, int j) { int temp = data[i]; data[i] = data[j]; data[j] = temp; } private static void subSort (int [] data, int start, int end) { if (start < end) { int base = data[start]; int low = start; int high = end + 1 ; while (true ) { while (low < end && data[++low] - base <= 0 ) ; while (high > start && data[--high] - base >= 0 ) ; if (low < high) { swap(data, low, high); } else { break ; } } swap(data, start, high); subSort(data, start, high - 1 ); subSort(data, high + 1 , end); } } public static void quickSort (int [] data) { subSort(data,0 ,data.length-1 ); } public static void main (String[] args) { int [] data = { 9 , -16 , 30 , 23 , -30 , -49 , 25 , 21 , 30 }; System.out.println("排序之前:\n" + java.util.Arrays.toString(data)); quickSort(data); System.out.println("排序之后:\n" + java.util.Arrays.toString(data)); } }
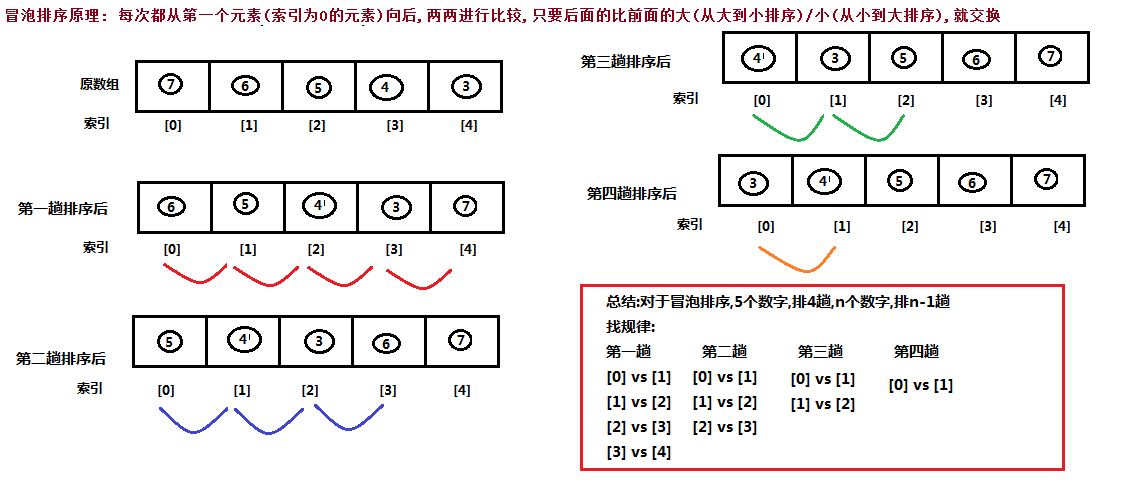
冒泡排序 冒泡排序概述
一种排序的方式,对要进行排序的数据中相邻的数据进行两两比较 ,将较大的数据放在后面,依次对所有的数据进行操作,直至所有数据按要求完成排序
如果有n个数据进行排序,总共需要比较n-1次
每一次比较完毕,下一次的比较就会少一个数据参与
冒泡排序图解
动图演示:
冒泡排序代码实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 排序思想: 1. 比较相邻的元素。如果第一个比第二个大(升序),就交换他们两个。2. 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。3. 针对所有的元素重复以上的步骤,除了最后一个。4. 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较为止。import java.util.Arrays;public class Test { public static void main (String[] args) { int [] arr = {7 , 6 , 18 , 5 , 4 , 3 }; System.out.println("排序前:" + Arrays.toString(arr)); for (int i = 0 ; i < arr.length - 1 ; i++) { for (int j = 0 ;j<arr.length-1 -i;j++){ if (arr[j] > arr[j+1 ]){ int temp = arr[j]; arr[j] = arr[j+1 ]; arr[j+1 ] = temp; } } } System.out.println("排序后:" + Arrays.toString(arr)); } }
选择排序 选择排序概述
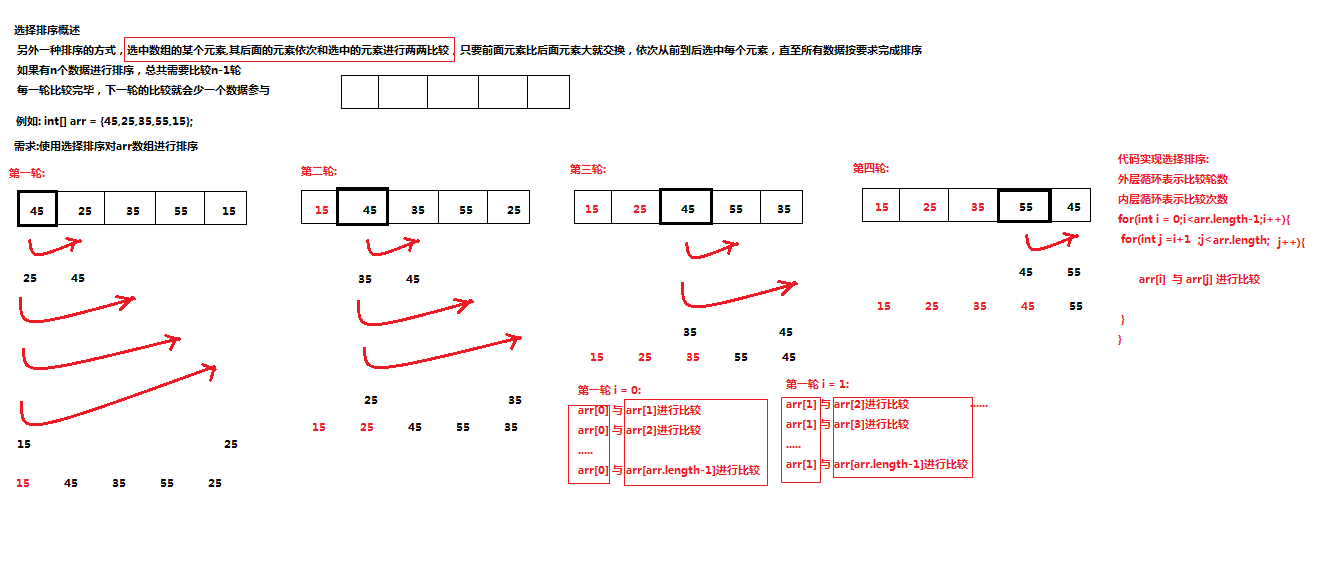
另外一种排序的方式,选中数组的某个元素,与其后面的元素依次进行两两比较,将较大的数据放在后面,依次从前到后选中每个元素,直至所有数据按要求完成排序
如果有n个数据进行排序,总共需要比较n-1轮
每一轮比较完毕,下一轮的比较就会少一个数据参与
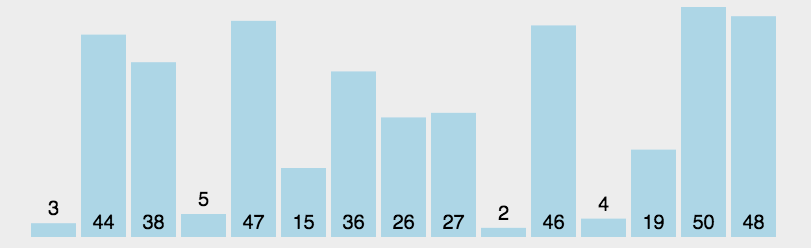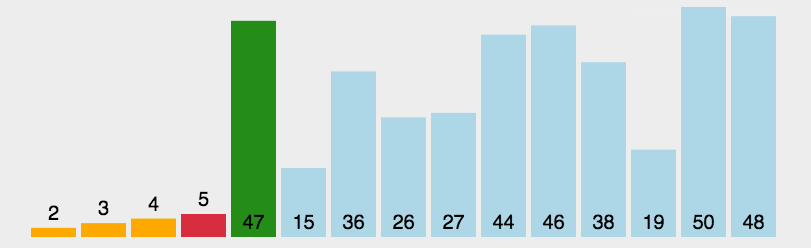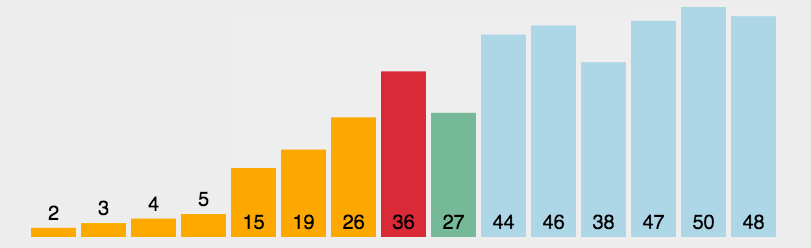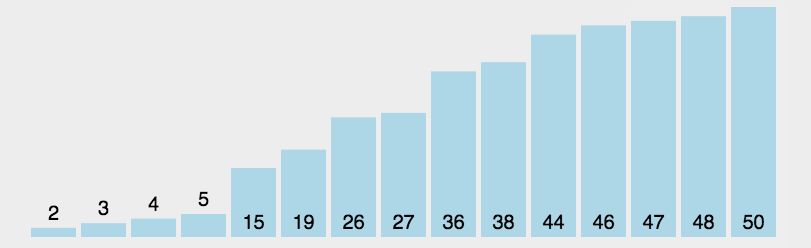
选择排序图解
动图演示:
选择排序代码实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 package com.itheima.demo2_选择排序;import java.util.Arrays;public class Test { public static void main (String[] args) { int [] arr = {45 , 25 , 35 , 55 , 15 }; System.out.println("排序前:" + Arrays.toString(arr)); for (int i = 0 ; i < arr.length - 1 ; i++) { for (int j = i + 1 ; j < arr.length; j++) { if (arr[i] > arr[j]){ int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } } } System.out.println("排序后:" + Arrays.toString(arr)); } }
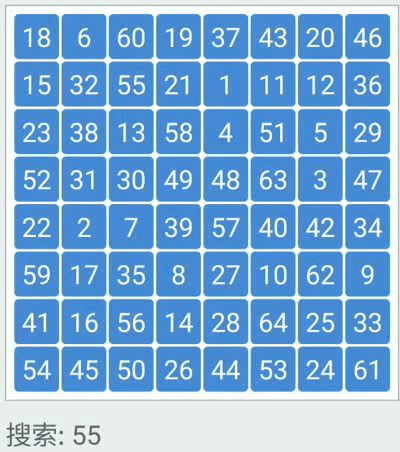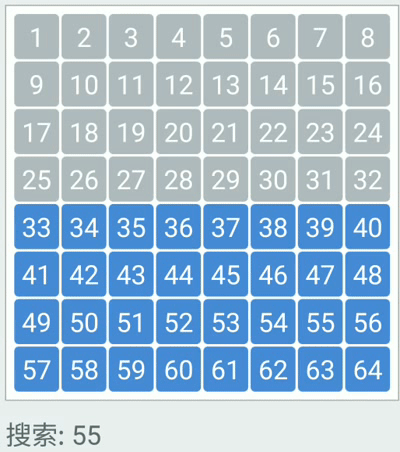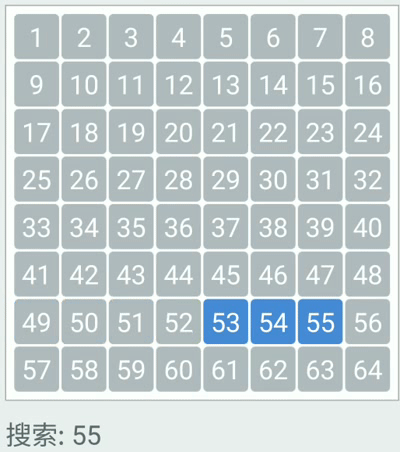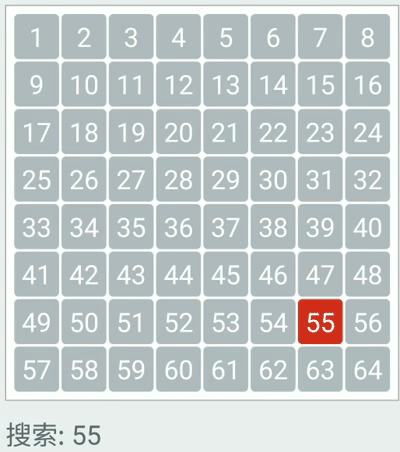
二分查找 普通查找 原理:遍历数组,获取每一个元素,然后判断当前遍历的元素是否和要查找的元素相同,如果相同就返回该元素的索引。如果没有找到,就返回一个负数作为标识(一般是-1)
二分查找原理 每一次都去获取数组的中间索引所对应的元素,然后和要查找的元素进行比对,如果相同就返回索引;
如果不相同,就比较中间元素和要查找的元素的值;
如果中间元素的值大于要查找的元素,说明要查找的元素在左侧,那么就从左侧按照上述思想继续查询(忽略右侧数据);
如果中间元素的值小于要查找的元素,说明要查找的元素在右侧,那么就从右侧按照上述思想继续查询(忽略左侧数据);
二分查找对数组是有要求的,数组必须已经排好序
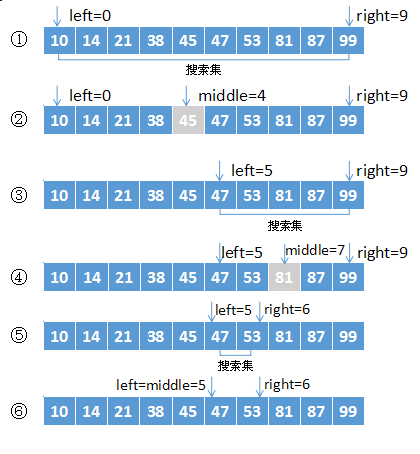
二分查找图解 假设有一个给定有序数组(10,14,21,38,45,47,53,81,87,99),要查找50出现的索引
则查询过程如下图所示:
动图演示:
二分查找代码实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public static void main (String[] args) { int [] arr = {10 , 14 , 21 , 38 , 45 , 47 , 53 , 81 , 87 , 99 }; int index = binarySerach(arr, 38 ); System.out.println(index); } public static int binarySerach (int [] arr, int number) { int start = 0 ; int end = arr.length - 1 ; while (start <= end) { int mid = (start + end) / 2 ; if (number == arr[mid]) { return mid ; } else if (number < arr[mid]) { end = mid - 1 ; } else if (number > arr[mid]) { start = mid + 1 ; } } return -1 ; }
权重均衡分配 请用java实现以下功能:
1 2 目前有N个员工,每个员工处理订单的能力不同,且这N个员工目前正在处理个数不等的订单,这时发来M个订单。 如何把M个订单分发到这N个员工中,使得分发完之后这N个员工所处理的订单是均衡的。
说明:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 package com.itheima;import java.util.*;public class Try { public static void main (String[] args) { int n = 10 ; List<Emp> empList = new ArrayList <Emp>(); int sum = 0 ; double sumX = 0.0 ; Emp emp = null ; for (int i = 0 ; i < n; i++){ emp = new Emp ("小强" + (i+1 ), (int )(Math.random() * 100 ), Math.random()); empList.add(emp); sum += emp.currentNum; sumX += emp.x; } int M = (int )(Math.random()*1000 ); for (Emp e : empList) { e.xPercentage = e.x/sumX; } while (true ) { emp = getMaxFreeEmp(empList,sum); emp.currentNum++; M--; emp.newAssigned++; if (M == 0 ){ break ; } sum++; } for (Emp computer : empList) { System.out.println(computer); } } public static Emp getMaxFreeEmp (List<Emp> emps,long sumNum) { Emp minEmp = null ; for (Emp emp : emps) { emp.avgNum = Math.round(sumNum * emp.xPercentage); emp.weight = emp.currentNum - emp.avgNum; if (minEmp == null ){ minEmp = emp; }else if (minEmp.weight > emp.weight){ minEmp = emp; } } return minEmp; } } class Emp { String name; long currentNum; long orgNum = 0 ; double x; long avgNum; long newAssigned=0 ; long weight = 0 ; double xPercentage = 0 ; public Emp (String _name, int _currentNum,double _x) { this .currentNum = _currentNum; this .orgNum = _currentNum; this .name = _name; this .x = _x; } @Override public String toString () { return "Computer{" + "name='" + name + '\'' + ", currentNum=" + currentNum + ", orgNum=" + orgNum + ", x=" + x + ", avgNum=" + avgNum + ", newAssigned=" + newAssigned + ", weight=" + weight + ", xPercentage=" + xPercentage + '}' ; } }
基于数据结构和算法的深入应用
回顾数据结构与算法的基础知识
学习日常所接触场景中的一些算法和策略
这些算法的原理和他背后的思想
动手写代码,用java里的数据结构来实现这些算法,如何去做?
1 概论 1.1 概念回顾 1.1.1 数据结构 1)概述
数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。
2)划分
从关注的维度看,数据结构可以划分为数据的逻辑结构和物理结构,同一逻辑结构可以对应不同的存储结构。
逻辑结构反映的是数据元素之间的逻辑关系,逻辑关系是指数据元素之间的前后间以什么形式相互关联,这与他们在计算机中的存储位置无关。逻辑结构包括:
集合:只是扎堆凑在一起,没有互相之间的关联
线性结构:一对一关联,队形
树形结构:一对多关联,树形
图形结构:多对多关联,网状
数据物理结构指的是逻辑结构在计算机存储空间中的存放形式(也称为存储结构)。一般来说,一种数据结构的逻辑结构根据需要可以表示成多种存储结构,常用的存储结构有顺序存储、链式存储、索引存储和哈希存储等。
顺序存储:用一组地址连续的存储单元依次存储集合的各个数据元素,可随机存取,但增删需要大批移动
链式存储:不要求连续,每个节点都由数据域和指针域组成,占据额外空间,增删快,查找慢需要遍历
索引存储:除建立存储结点信息外,还建立附加的索引表来标识结点的地址。检索快,空间占用大
哈希存储:将数据元素的存储位置与关键码之间建立确定对应关系,检索快,存在映射函数碰撞问题
3)程序中常见的数据结构
数组(Array):连续存储,线性结构,可根据偏移量随机读取,扩容困难
栈( Stack):线性存储,只允许一端操作,先进后出,类似水桶
队列(Queue):类似栈,可以双端操作。先进先出,类似水管
链表( LinkedList):链式存储,配备前后节点的指针,可以是双向的
树( Tree):典型的非线性结构,从唯一的根节点开始,子节点单向执行前驱(父节点)
图(Graph):另一种非线性结构,由节点和关系组成,没有根的概念,互相之间存在关联
堆(Heap):特殊的树,特点是根结点的值是所有结点中最小的或者最大的,且子树也是堆
散列表(Hash):源自于散列函数,将值做一个函数式映射,映射的输出作为存储的地址
1.1.2 算法 算法指的是基于存储结构下,对数据如何有效的操作,采用什么方式可以更有效的处理数据,提高数据运算效率。数据的运算是定义在数据的逻辑结构上,但运算的具体实现要在存储结构上进行。一般涉及的操作有以下几种:
检索:在数据结构里查找满足一定条件的节点。
插入:往数据结构中增加新的节点,一般有一点位置上的要求。
删除:把指定的结点从数据结构中去掉,本身可能隐含有检索的需求。
更新:改变指定节点的一个或多个字段的值,同样隐含检索。
排序:把节点里的数据,按某种指定的顺序重新排列,例如递增或递减。
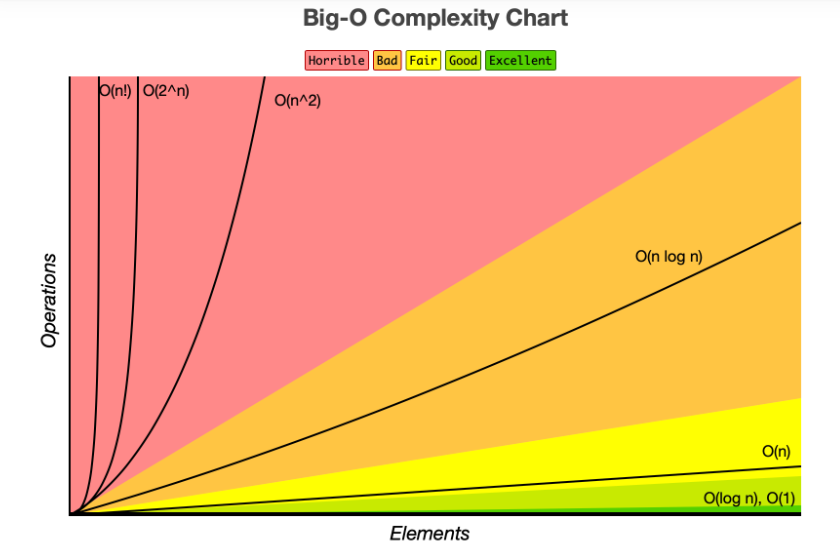
1.2 复杂度 - 【拓展】 1.2.1 时间复杂度 简单理解,为了某种运算而花费的时间,使用大写O表示。一般来讲,时间是一个不太容易计量的维度,而为了计算时间复杂度,通常会估计算法的操作单元数量,而假定每个单元运行的时间都是相同的。因此,总运行时间和算法的操作单元数量一般来讲成正比,最多相差一个常量系数。一般来讲,常见时间复杂度有以下几种:
1)常数阶O(1):时间与数据规模无关,如交换两个变量值
1 2 int i=1 ,j=2 ,kk=i;i=j;j=k;
2)线性阶O(n):时间和数据规模呈线性,可以理解为n的1次方,如单循环里的操作
1 2 3 for (i=1 ;i<=n;i++){ do (); }
3)k次方阶O(nk):执行次数是数量的k次方,如多重循环,以下为2次方阶实例
1 2 3 4 5 for (i=1 ;i<=n;i++){ for (j=1 ;j<=n;j++){ do (); } }
4)指数阶O(2n):随着n的上升,运算次数呈指数增长
1 2 3 for (i=1 ;i<= 2 ^n;i++){ do (); }
5)对数阶O(log2n):执行次数呈对数缩减,如下
1 2 3 4 for (i=1 ;i<=n;){ i=2 ^i; do (); }
6)线性对数阶O(nlog2n):在对数阶的基础上,进行线性n倍乘积
1 2 3 4 5 for (i=1 ;i<=2 ^n;i++){ for (j=1 ;j<=n;j++){ do (); } }
7)总结:
时间复杂度由小到大依次为:Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<...<Ο(nk)<Ο(2n)<Ο(n!)
1.2.2 空间复杂度 与时间复杂度类似,空间复杂度是对一个算法在运行过程中占用内存空间大小的度量。一个程序执行时除了需要存储空间和存储本身所使用的指令、常数、变量和输入数据外,还需要一些对数据进行操作的辅助空间。而空间复杂度主要指的是这部分空间的量级。
同样,空间复杂度也用大写O表示,相比时间复杂度场景相对简单,常见级别为O(1)和O(n),以数组逆序为例,两种不同算法对复杂度影响如下:
1)O(1):常数阶,所占空间和数据量大小无关。
1 2 3 4 5 6 7 8 9 10 11 int [] a={1 ,2 ,3 ,4 ,5 };int i=0 ,j=a.length-1 ;while (i<=j){ int temp = a[i]; a[i]=a[j]; a[j]=temp; i++; j--; }
2)O(n):线性阶,与数据量大小呈线性关系
1 2 3 4 5 6 7 int [] a={1 ,2 ,3 ,4 ,5 };int [] b=new int [a.length];for (int i = 0 ; i < a.length; i++) { b[i]=a[a.length-1 -i]; }
1.2.3 类比 对于一个算法,其时间复杂度和空间复杂度往往是相互影响的。时间复杂度低可能借助占用大的存储空间来弥补,反之,某个算法所占据空间小,那么可能就需要占用更多的运算时间。两者往往需要达到一种权衡。
在特定环境下的业务,还需要综合考虑算法的各项性能,如使用频率,数据量的大小,所用的开发语言,运行的机器系统等。两者兼顾权衡利弊才能设计出最适合当前场景的算法。
1.3 算法思想 - 【拓展】 1.3.1 分而治之 把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题,直到最后子问题小到可以简单的直接求解,原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础,如排序算法(快速排序,归并排序),傅立叶变换(快速傅立叶变换),大数据中的MR,现实中如汉诺塔游戏。
分治法对问题有一定的要求:
该问题缩小到一定程度后,就可以轻松解决
问题具有可拆解性,不是一团无法拆分的乱麻
拆解后的答案具有可合并性。能组装成最终结果
拆解的子问题要相互独立,互相之间不存在或者很少有依赖关系
1.3.2 动态规划 基本思想与分治法类似,也是将待求解的问题分解为若干个子问题(阶段),按顺序求解子阶段,前一子问题的解,为后一子问题的求解提供了有用的信息。在求解任一子问题时,列出各种可能的局部解,通过决策保留那些有可能达到最优的局部解,丢弃其他。依次解决各子问题,最后一个子问题就是初始问题的解。
与分治法最大的不同在于,分治法的思想是并发,动态规划的思想是分步 。该方法经分解后得到的子问题往往不是互相独立的,其下一个子阶段的求解往往是建立在上一个子阶段的解的基础上。动态规划算法同样有一定的适用性场景要求:
最优化解:拆解后的子阶段具备最优化解,且该最优化解与追踪答案方向一致
流程向前,无后效性:上一阶段的解决方案一旦确定,状态就确定,只会影响下一步,而不会反向影响
阶段关联:上下阶段不是独立的,上一阶段会对下一阶段的行动提供决策性指导。这不是必须的,但是如果具备该特征,动态规划算法的意义才能更大的得到体现
1.3.3 贪心算法 同样对问题要求作出拆解,但是每一步,以当前局部为目标,求得该局部的最优解。那么最终问题解决时,得到完整的最优解。也就是说,在对问题求解时,总是做出在当前看来是最好的选择,而不去从整体最优上加以考虑。从这一角度来讲,该算法具有一定的场景局限性。
要求问题可拆解,并且拆解后每一步的状态无后效性(与动态规划算法类似)
要求问题每一步的局部最优,与整体最优解方向一致。至少会导向正确的主方向。
1.3.4 回溯算法 回溯算法实际上是一个类似枚举的搜索尝试过程,在每一步的问题下,列举可能的解决方式。选择某个方案往深度探究,寻找问题的解,当发现已不满足求解条件,或深度达到一定数量时,就返回,尝试别的路径。回溯法一般适用于比较复杂的,规模较大的问题。有“通用解题法”之称。
问题的解决方案具备可列举性,数量有限
界定回溯点的深度。达到一定程度后,折返
1.3.5 分支限界 与回溯法类似,也是一种在空间上枚举寻找最优解的方式。但是回溯法策略为深度优先。分支法为广度优先 。分支法一般找到所有相邻结点,先采取淘汰策略,抛弃不满足约束条件的结点,其余结点加入活结点表。然后从存活表中选择一个结点作为下一个操作对象。
1.4 总结
针对算法做了相应的回顾
算法的考量:时间与空间复杂度
算法的基本思想
2 失效算法与应用 失效算法常见于缓存系统中。因为缓存往往占据大量内存,而内存空间是相对昂贵,且空间有限的,那么针对一部分值,就要依据相应的算法进行失效或移除操作。
2.1 先来先淘汰(FIFO) 1)概述
First In First Out,先来先淘汰。这种算法在每一次新数据插入时,如果队列已满,则将最早插入的数据移除。
2)实现
可以方便的借助LinkedList来实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 package com.itheima.release;import java.util.Iterator;import java.util.LinkedList;public class FIFO { LinkedList<Integer> fifo = new LinkedList <Integer>(); int size = 3 ; public void add (int i) { fifo.addFirst(i); if (fifo.size() > size){ fifo.removeLast(); } print(); } public void read (int i) { Iterator<Integer> iterator = fifo.iterator(); while (iterator.hasNext()){ int j = iterator.next(); if (i == j){ System.out.println("find it!" ); print(); return ; } } System.out.println("not found!" ); print(); } public void print () { System.out.println(this .fifo); } public static void main (String[] args) { FIFO fifo = new FIFO (); System.out.println("add 1-3:" ); fifo.add(1 ); fifo.add(2 ); fifo.add(3 ); System.out.println("add 4:" ); fifo.add(4 ); System.out.println("read 2:" ); fifo.read(2 ); System.out.println("read 100:" ); fifo.read(100 ); System.out.println("add 5:" ); fifo.add(5 ); } }
3)结果分析
1-3按顺序放入,没有问题
4放入,那么1最早放入,被挤掉
读取2,读到,但是不会影响队列顺序(2依然是时间最老的)
读取100,读不到,也不会产生任何影响
5加入,踢掉了2,而不管2之前有没有被使用(不够理性)
4)优缺点
实现非常简单
不管元素的使用情况,哪怕有些数据会被频繁用到,时间最久也会被踢掉
2.2 最久未用淘汰(LRU) 1)概述
LRU全称是Least Recently Used,即淘汰最后一次使用时间最久远的数值。FIFO非常的粗暴,不管有没有用到,直接踢掉时间久的元素。而LRU认为,最近频繁使用过的数据,将来也很大程度上会被频繁用到,故而淘汰那些懒惰的数据。LinkedHashMap,数组,链表均可实现LRU,下面仍然以链表为例:新加入的数据放在头部,最近访问的,也移到头部,空间满时,将尾部元素删除。
2)实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 package com.itheima.release;import java.util.Iterator;import java.util.LinkedList;public class LRU { LinkedList<Integer> lru = new LinkedList <Integer>(); int size = 3 ; public void add (int i) { lru.addFirst(i); if (lru.size() > size){ lru.removeLast(); } print(); } public void read (int i) { Iterator<Integer> iterator = lru.iterator(); int index = 0 ; while (iterator.hasNext()){ int j = iterator.next(); if (i == j){ System.out.println("find it!" ); lru.remove(index); lru.addFirst(j); print(); return ; } index++; } System.out.println("not found!" ); print(); } public void print () { System.out.println(this .lru); } public static void main (String[] args) { LRU lru = new LRU (); System.out.println("add 1-3:" ); lru.add(1 ); lru.add(2 ); lru.add(3 ); System.out.println("add 4:" ); lru.add(4 ); System.out.println("read 2:" ); lru.read(2 ); System.out.println("read 100:" ); lru.read(100 ); System.out.println("add 5:" ); lru.add(5 ); } }
3)结果分析
1-3加入,没有问题
4加入,踢掉1,没问题
读取2,读到,注意,2被移到了队首!
读取100,读不到,没影响
5加入,因为2之前被用到,不会被剔除,3和4都没人用,但是3更久,被剔除
2.3 最近最少使用(LFU) 1)概述
Least Frequently Used,即最近最少使用。它要淘汰的是最近一段时间内,使用次数最少的值。可以认为比LRU多了一重判断。LFU需要时间和次数两个维度的参考指标。需要注意的是,两个维度就可能涉及到同一时间段内,访问次数相同的情况,就必须内置一个计数器和一个队列,计数器算数,队列放置相同计数时的访问时间。
2)实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 package com.itheima.release;public class Dto implements Comparable <Dto> { private Integer key; private int count; private long lastTime; public Dto (Integer key, int count, long lastTime) { this .key = key; this .count = count; this .lastTime = lastTime; } @Override public int compareTo (Dto o) { int compare = Integer.compare(this .count, o.count); return compare == 0 ? Long.compare(this .lastTime, o.lastTime) : compare; } @Override public String toString () { return String.format("[key=%s,count=%s,lastTime=%s]" ,key,count,lastTime); } public Integer getKey () { return key; } public void setKey (Integer key) { this .key = key; } public int getCount () { return count; } public void setCount (int count) { this .count = count; } public long getLastTime () { return lastTime; } public void setLastTime (long lastTime) { this .lastTime = lastTime; } }
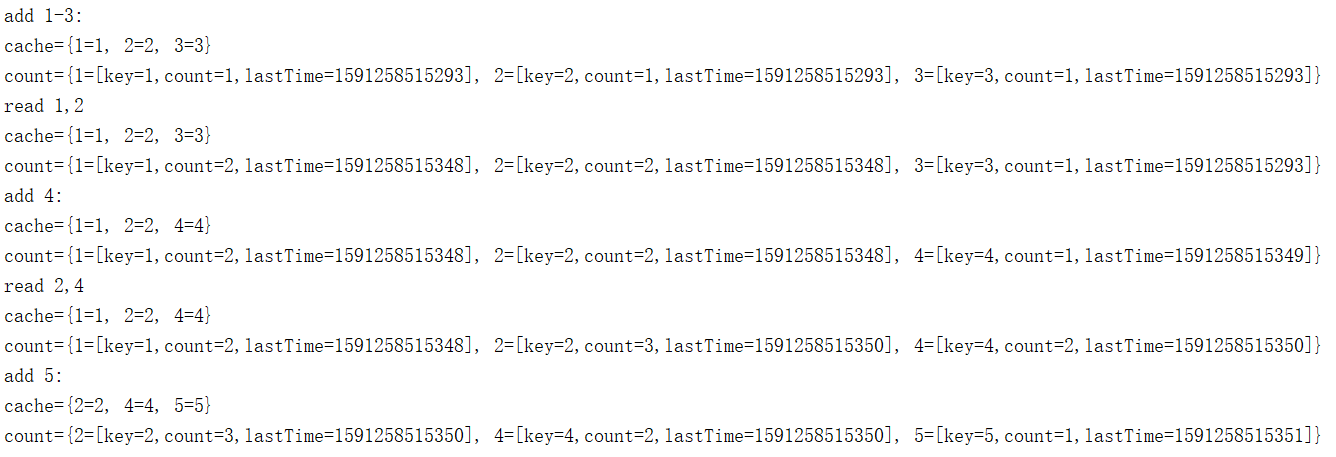
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 package com.itheima.release;import java.util.Collections;import java.util.HashMap;import java.util.Map;public class LFU { private final int size = 3 ; private Map<Integer,Integer> cache = new HashMap <>(); private Map<Integer, Dto> count = new HashMap <>(); public void put (Integer key, Integer value) { Integer v = cache.get(key); if (v == null ) { if (cache.size() == size) { removeElement(); } count.put(key, new Dto (key, 1 , System.currentTimeMillis())); } else { addCount(key); } cache.put(key, value); } public Integer get (Integer key) { Integer value = cache.get(key); if (value != null ) { addCount(key); return value; } return null ; } private void removeElement () { Dto dto = Collections.min(count.values()); cache.remove(dto.getKey()); count.remove(dto.getKey()); } private void addCount (Integer key) { Dto Dto = count.get(key); Dto.setCount(Dto.getCount()+1 ); Dto.setLastTime(System.currentTimeMillis()); } private void print () { System.out.println("cache=" +cache); System.out.println("count=" +count); } public static void main (String[] args) { LFU lfu = new LFU (); System.out.println("add 1-3:" ); lfu.put(1 , 1 ); lfu.put(2 , 2 ); lfu.put(3 , 3 ); lfu.print(); System.out.println("read 1,2" ); lfu.get(1 ); lfu.get(2 ); lfu.print(); System.out.println("add 4:" ); lfu.put(4 , 4 ); lfu.print(); System.out.println("read 2,4" ); lfu.get(2 ); lfu.get(4 ); lfu.print(); System.out.println("add 5:" ); lfu.put(5 , 5 ); lfu.print(); } }
3)结果分析
1-3加入,没问题,计数器为1次
访问1,2,使用次数计数器上升为2次,3没有访问,仍然为1
4加入,3的访问次数最少(1次),所以踢掉3,剩下124
访问2,4,计数器上升,2=3次,1,4=2次,但是1时间久
5加入,踢掉1,最后剩下2,4,5
2.4 应用案例 redis属于缓存失效的典型应用场景,常见策略如下:
noeviction: 不删除策略, 达到最大内存限制时, 如果需要更多内存, 直接返回错误信息( 比较危险)。
allkeys-lru:对所有key,优先删除最近最少使用的 key (LRU)。
allkeys-random: 对所有key, 随机删除一部分(听起来毫无道理)。
volatile-lru:只限于设置了 expire 的key,优先删除最近最少使用的key (LRU)。
volatile-random:只限于设置了 expire 的key,随机删除一部分。
volatile-ttl:只限于设置了 expire 的key,优先删除剩余时间(TTL) 短的key。
3 限流算法与应用 限流是对系统的一种保护措施。即限制流量请求的频率(每秒处理多少个请求)。一般来说,当请求流量超过系统的瓶颈,则丢弃掉多余的请求流量,保证系统的可用性。即要么不放进来,放进来的就保证提供服务。
3.1 计数器 1)概述
计数器采用简单的计数操作,到一段时间节点后自动清零
2)实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 package com.itheima.limit;import java.util.concurrent.*;public class Counter { public static void main (String[] args) { final Semaphore semaphore = new Semaphore (3 ); ScheduledExecutorService service = Executors.newScheduledThreadPool(1 ); service.scheduleAtFixedRate(new Runnable () { @Override public void run () { semaphore.release(3 ); } },3000 ,3000 ,TimeUnit.MILLISECONDS); while (true ) { try { semaphore.acquire(); } catch (InterruptedException e) { e.printStackTrace(); } System.out.println("ok" ); } } }
3)结果分析
4)优缺点
实现起来非常简单。
控制力度太过于简略,假如1s内限制3次,那么如果3次在前100ms内已经用完,后面的900ms将只能处于阻塞状态,白白浪费掉。
5)应用
使用计数器限流的场景较少,因为它的处理逻辑不够灵活。最常见的可能在web的登录密码验证,输入错误次数冻结一段时间的场景。如果网站请求使用计数器,那么恶意攻击者前100ms吃掉流量计数,使得后续正常的请求被全部阻断,整个服务很容易被搞垮。
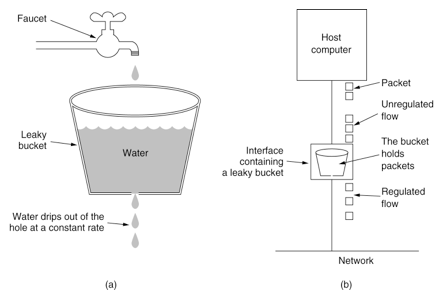
3.2 漏桶算法 1)概述
漏桶算法将请求缓存在桶中,服务流程匀速处理。超出桶容量的部分丢弃。漏桶算法主要用于保护内部的处理业务,保障其稳定有节奏的处理请求,但是无法根据流量的波动弹性调整响应能力。现实中,类似容纳人数有限的服务大厅开启了固定的服务窗口。
2)实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 package com.itheima.limit;import java.util.concurrent.*;public class Barrel { public static void main (String[] args) { final LinkedBlockingQueue<Integer> que = new LinkedBlockingQueue (3 ); ScheduledExecutorService service = Executors.newScheduledThreadPool(1 ); service.scheduleAtFixedRate(new Runnable () { @Override public void run () { int v = que.poll(); System.out.println("处理:" +v); } },2000 ,2000 ,TimeUnit.MILLISECONDS); int i=0 ; while (true ) { i++; try { System.out.println("put:" +i); que.offer(i,1000 ,TimeUnit.MILLISECONDS); } catch (Exception e) { e.printStackTrace(); } } } }
3)结果分析
put任务号按照顺序入桶
执行任务匀速的1s一个被处理
因为桶的容量只有3,所以1-3完美执行,4被溢出丢弃,5正常执行
4)优缺点
有效的挡住了外部的请求,保护了内部的服务不会过载
内部服务匀速执行,无法应对流量洪峰,无法做到弹性处理突发任务
任务超时溢出时被丢弃。现实中可能需要缓存队列辅助保持一段时间
5)应用
nginx中的限流是漏桶算法的典型应用,配置案例如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 http { limit_req_zone $binary_remote_addr zone=one:10m rate=1r/s; server { location /limited/ { limit_req zone=one burst=5 nodelay; } }
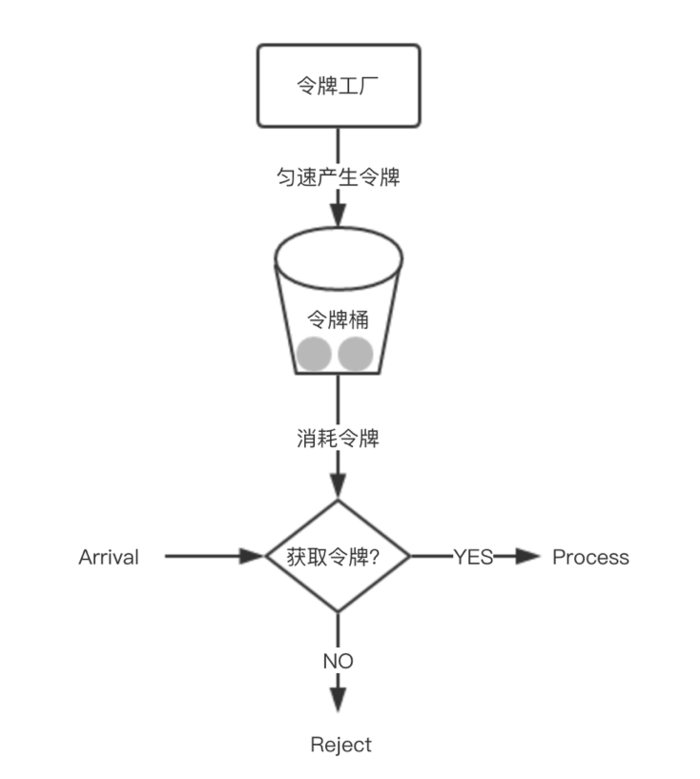
3.3 令牌桶 1)概述
令牌桶算法可以认为是漏桶算法的一种升级,它不但可以将流量做一步限制,还可以解决漏桶中无法弹性伸缩处理请求的问题。体现在现实中,类似服务大厅的门口设置门禁卡发放。发放是匀速的,请求较少时,令牌可以缓存起来,供流量爆发时一次性批量获取使用。而内部服务窗口不设限。
2)实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 package com.itheima.limit; import java.util.concurrent.*; public class Token { public static void main(String[] args) throws InterruptedException { //令牌桶,信号量实现,容量为3 final Semaphore semaphore = new Semaphore(3); //定时器,1s一个,匀速颁发令牌 ScheduledExecutorService service = Executors.newScheduledThreadPool(1); service.scheduleAtFixedRate(new Runnable() { @Override public void run() { if (semaphore.availablePermits() < 3){ semaphore.release(); } // System.out.println("令牌数:"+semaphore.availablePermits()); } },1000,1000,TimeUnit.MILLISECONDS); //等待,等候令牌桶储存 Thread.sleep(5); //模拟洪峰5个请求,前3个迅速响应,后两个排队 for (int i = 0; i < 5; i++) { semaphore.acquire(); System.out.println("洪峰:"+i); } //模拟日常请求,2s一个 for (int i = 0; i < 3; i++) { Thread.sleep(1000); semaphore.acquire(); System.out.println("日常:"+i); Thread.sleep(1000); } //再次洪峰 for (int i = 0; i < 5; i++) { semaphore.acquire(); System.out.println("洪峰:"+i); } //检查令牌桶的数量 for (int i = 0; i < 5; i++) { Thread.sleep(2000); System.out.println("令牌剩余:"+semaphore.availablePermits()); } } }
3)结果分析
注意结果出现的节奏!
洪峰0-2迅速被执行,说明桶中暂存了3个令牌,有效应对了洪峰
洪峰3,4被间隔性执行,得到了有效的限流
日常请求被匀速执行,间隔均匀
第二波洪峰来临,和第一次一样
请求过去后,令牌最终被均匀颁发,积累到3个后不再上升
4)应用
springcloud中gateway可以配置令牌桶实现限流控制,案例如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 cloud: gateway: routes: - id: limit_route uri: http://localhost:8080/test filters: - name: RequestRateLimiter args: #限流的key,ipKeyResolver为spring中托管的Bean,需要扩展KeyResolver接口 key-resolver: '#{@ipResolver}' #令牌桶每秒填充平均速率,相当于代码中的发放频率 redis-rate-limiter.replenishRate: 1 #令牌桶总容量,相当于代码中,信号量的容量 redis-rate-limiter.burstCapacity: 3
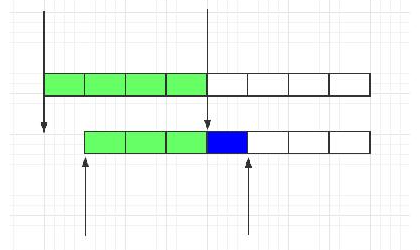
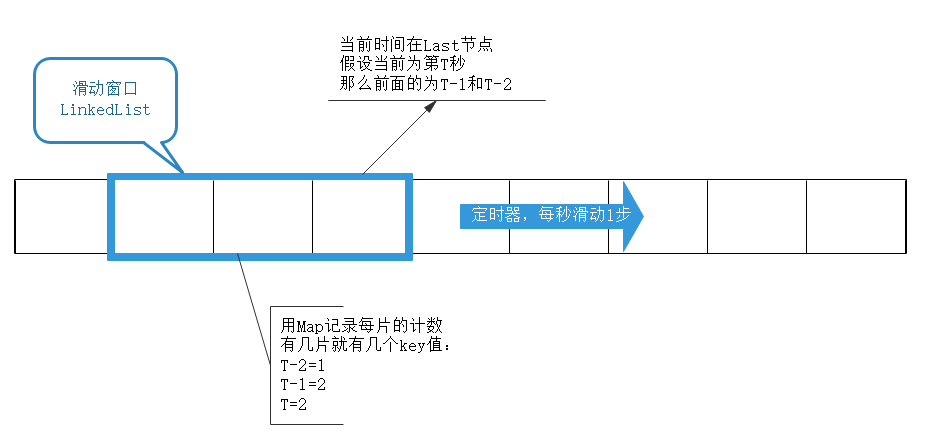
3.4 滑动窗口 1)概述
滑动窗口可以理解为细分之后的计数器,计数器粗暴的限定1分钟内的访问次数,而滑动窗口限流将1分钟拆为多个段,不但要求整个1分钟内请求数小于上限,而且要求每个片段请求数也要小于上限。相当于将原来的计数周期做了多个片段拆分。更为精细。
2)实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 package com.itheima.limit; import java.util.LinkedList; import java.util.Map; import java.util.TreeMap; import java.util.concurrent.Executors; import java.util.concurrent.ScheduledExecutorService; import java.util.concurrent.TimeUnit; import java.util.concurrent.atomic.AtomicInteger; public class Window { //整个窗口的流量上限,超出会被限流 final int totalMax = 5; //每片的流量上限,超出同样会被拒绝,可以设置不同的值 final int sliceMax = 5; //分多少片 final int slice = 3; //窗口,分3段,每段1s,也就是总长度3s final LinkedList<Long> linkedList = new LinkedList<>(); //计数器,每片一个key,可以使用HashMap,这里为了控制台保持有序性和可读性,采用TreeMap Map<Long,AtomicInteger> map = new TreeMap(); //心跳,每1s跳动1次,滑动窗口向前滑动一步,实际业务中可能需要手动控制滑动窗口的时机。 ScheduledExecutorService service = Executors.newScheduledThreadPool(1); //获取key值,这里即是时间戳(秒) private Long getKey(){ return System.currentTimeMillis()/1000; } public Window(){ //初始化窗口,当前时间指向的是最末端,前两片其实是过去的2s Long key = getKey(); for (int i = 0; i < slice; i++) { linkedList.addFirst(key-i); map.put(key-i,new AtomicInteger(0)); } //启动心跳任务,窗口根据时间,自动向前滑动,每秒1步 service.scheduleAtFixedRate(new Runnable() { @Override public void run() { Long key = getKey(); //队尾添加最新的片 linkedList.addLast(key); map.put(key,new AtomicInteger()); //将最老的片移除 map.remove(linkedList.getFirst()); linkedList.removeFirst(); System.out.println("step:"+key+":"+map);; } },1000,1000,TimeUnit.MILLISECONDS); } //检查当前时间所在的片是否达到上限 public boolean checkCurrentSlice(){ long key = getKey(); AtomicInteger integer = map.get(key); if (integer != null){ return integer.get() < sliceMax ; } //默认允许访问 return true; } //检查整个窗口所有片的计数之和是否达到上限 public boolean checkAllCount(){ return map.values().stream().mapToInt(value -> value.get()).sum() < totalMax; } //请求来临.... public void req(){ Long key = getKey(); //如果时间窗口未到达当前时间片,稍微等待一下 //其实是一个保护措施,放置心跳对滑动窗口的推动滞后于当前请求 while (linkedList.getLast()<key){ try { Thread.sleep(200); } catch (InterruptedException e) { e.printStackTrace(); } } //开始检查,如果未达到上限,返回ok,计数器增加1 //如果任意一项达到上限,拒绝请求,达到限流的目的 //这里是直接拒绝。现实中可能会设置缓冲池,将请求放入缓冲队列暂存 if (checkCurrentSlice() && checkAllCount()){ map.get(key).incrementAndGet(); System.out.println(key+"=ok:"+map); }else { System.out.println(key+"=reject:"+map); } } public static void main(String[] args) throws InterruptedException { Window window = new Window(); //模拟10个离散的请求,相对之间有200ms间隔。会造成总数达到上限而被限流 for (int i = 0; i < 10; i++) { Thread.sleep(200); window.req(); } //等待一下窗口滑动,让各个片的计数器都置零 Thread.sleep(3000); //模拟突发请求,单个片的计数器达到上限而被限流 System.out.println("---------------------------"); for (int i = 0; i < 10; i++) { window.req(); } } }
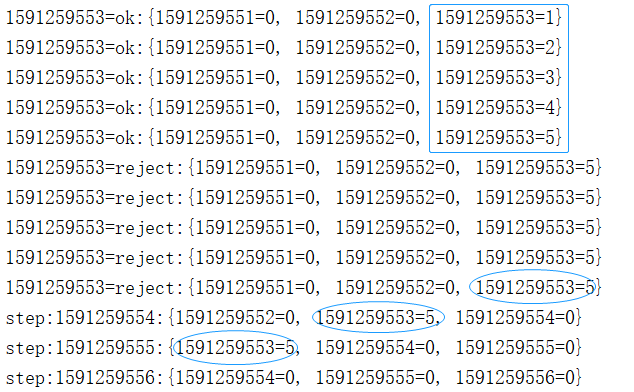
3)结果分析
模拟零零散散的请求,会造成每个片里均有计数,总数达到上限后,不再响应,限流生效:
再模拟突发的流量请求,会造成单片流量计数达到上限,不再响应而被限流
4)应用
滑动窗口算法,在tcp协议发包过程中被使用。在web现实场景中,可以将流量控制做更细化处理,解决计数器模型控制力度太粗暴的问题。
4 调度算法与应用 调度算法常见于操作系统中,因为系统资源有限,当有多个进程(或多个进程发出的请求)要使用这些资源时,就必须按照一定的原则选择进程(请求)来占用资源。这就是所谓的调度。在现实生活中也是一样,比如会议室的占用。
4.1 先来先服务(FCFS)- 【拓展】 1)概念
先来先服务,很好理解,就是按照服务提交申请的顺序,依次执行。讲究先来后到。
2)实现
定义一个Task类作为任务实例,BlockingQueue作为服务队列
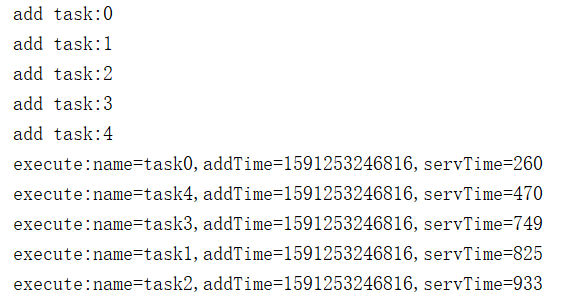
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 package com.itheima.schedule; /** * 任务类 */ public class Task { //任务名称 private String name; //任务提交的时间 private Long addTime; //任务的执行时间长短 private int servTime; public Task(String name, int servTime) { this.name = name; this.servTime = servTime; this.addTime = System.currentTimeMillis(); } public void execute() { try { // !重点:执行时睡眠,表示该任务耗时servTime毫秒 Thread.currentThread().sleep(servTime); } catch (InterruptedException e) { e.printStackTrace(); } System.out.println(String.format("execute:name=%s,addTime=%s,servTime=%s", name, addTime, servTime)); } } package com.itheima.schedule; import java.util.Random; import java.util.concurrent.LinkedBlockingQueue; public class FCFS { public static void main(String[] args) throws InterruptedException { //阻塞队列,FCFS的基础 final LinkedBlockingQueue<Task> queue = new LinkedBlockingQueue(5); //服务线程,任务由该线程获取和执行 new Thread(new Runnable(){ @Override public void run() { while (true) { try { queue.take().execute(); } catch (Exception e) { e.printStackTrace(); } } } }).start(); //向队列中放入一个任务 for (int i = 0; i < 5; i++) { System.out.println("add task:"+i); queue.put(new Task("task"+i,new Random().nextInt(1000))); } } }
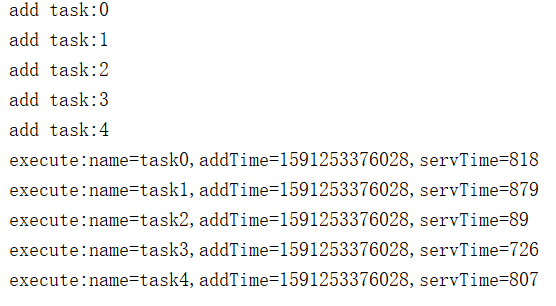
3)结果分析
4)优缺点
多应用于cpu密集型任务场景,对io密集型的不利。
时间相对均衡的业务可以排队处理,比如现实中排队打卡进站。
如果业务需要依赖大量的外部因素,执行时间片长短不一,FCFS算法不利于任务的整体处理进度,可能会因为一个长时间业务的阻塞而造成大量等待。
4.2 短作业优先 (SJF) 1)概念
执行时间短的优先得到资源。即执行前申报一个我需要占据cpu的时间,根据时间长短,短的优先被调度。我不占时间所以我先来。
2)实现
使用TreeMap可以实现优先级的任务排序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 package com.itheima.schedule; import javax.swing.text.html.parser.Entity; import java.util.Map; import java.util.Random; import java.util.TreeMap; public class SJF { public static void main(String[] args) throws InterruptedException { //有序Map,将服务时间作为key排序 final TreeMap<Integer,Task> treeMap = new TreeMap(); //向队列中放入5个任务 for (int i = 0; i < 5; i++) { System.out.println("add task:"+i); int servTime = new Random().nextInt(1000); //注意,key是servTime,即执行预估时间 treeMap.put(servTime,new Task("task"+i,servTime)); } //服务线程,任务由该线程获取和执行 new Thread(new Runnable(){ @Override public void run() { while (true) { try { //有序Map中,服务时间短的,置于顶部,那么自然就会优先被取出 Map.Entry<Integer,Task> entry = treeMap.pollFirstEntry(); if (entry == null){ Thread.currentThread().sleep(100); }else { entry.getValue().execute(); } } catch (Exception e) { e.printStackTrace(); } } } }).start(); } }
3)结果分析
4)优缺点
适用于任务时间差别较大的场景,仍然以进站为例,拿出公交卡的优先刷卡,还没办卡的让一让。
解决了
整体处理时间长的问题,降低平均等待时间,提高了系统吞吐量。
未考虑作业的紧迫程度,因而不能保证紧迫性作业(进程)的及时处理
对长作业的不利,可能等待很久而得不到执行
时间基于预估和申报,主观性因素在内,无法做到100%的精准
4.3 时间片轮转(RR) 1)概念
时间片逐个扫描轮询,轮到谁谁执行。大家公平裁决来者有份,谁也别插队。像是棋牌游戏中的发牌操作,做到了时间和机会上的平均性。
2)实现
基于数组做为数据插槽方式实现。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 package com.itheima.schedule; import java.util.Random; public class RR { //定义数组作为插槽,每个插槽中可以放入任务 Integer[] integers; //length插槽的个数 public RR(int length){ integers = new Integer[length]; } //将任务放入插槽 public void addTask(int value){ int slot = 0; //不停查找空的插槽 while (true) { //发现空位,将当前任务放入 if (integers[slot] == null){ integers[slot] = value; System.out.println(String.format("------------------------->add task index=%s,value=%s",slot,value)); break; } //如果当前位置有任务占用,看下一个位置 slot++; //如果插槽遍历完还是没有空位置,那么从头开始再找,继续下一个轮回 if (slot == integers.length){ slot = 0; } } } //执行任务。轮询的策略就在这里 public void execute(){ //开启一个线程处理任务。在现实中可能有多个消费者来处理 new Thread(new Runnable() { @Override public void run() { int index = 0; while (true) { //指针轮询,如果到达尾部,下一步重新转向开头 // 数据物理结构是一个数组,逻辑上是一个环 if (index == integers.length){ index = 0; } //如果当前位置没有任务,轮询到下一个插槽 if (integers[index] == null){ index++; continue; }else{ //随机等待,表示模拟当前任务有一个执行时间 try { Thread.currentThread().sleep(new Random().nextInt(1000)); } catch (InterruptedException e) { e.printStackTrace(); } //模拟任务执行的内容,也就是打印一下当前插槽和里面的值 System.out.println(String.format("execute index=%s,value=%s",index,integers[index])); //执行完,将当前插槽清空,腾出位置来给后续任务使用 integers[index] = null; } } } }).start(); } public static void main(String[] args) { //测试开始,定义3个插槽 RR rr = new RR(3); //唤起执行者线程,开始轮询 rr.execute(); //放置10个任务 for (int i = 0; i < 10; i++) { rr.addTask(i); } } }
3)结果分析
add任务index无序,value有序,说明是按顺序提交的,但是插槽无序,哪里有空放哪里
execute执行index有序value无序,说明任务是轮询执行的,每个插槽里的任务不一定是谁
4)优缺点
做到了机会的相对平均,不会因为某个任务执行时间超长而永远得不到执行
缺乏任务主次的处理。重要的任务无法得到优先执行,必须等到时间片轮到自己,着急也没用
4.4 优先级调度(HPF) - 【拓展】 1)概述
进程调度每次将处理机分配给具有最高优先级的就绪进程。最高优先级算法可与不同的CPU方式结合形成可抢占式最高优先级算法和不可抢占式最高优先级算法。
2)实现
在Task类中新增一个属性level作为优先级标识
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 package com.itheima.schedule; /** * 任务类 */ public class Task { //任务名称 private String name; //任务提交的时间 private Long addTime; //任务的执行时间 private int servTime; //任务优先级 private int level; public Task(String name, int servTime) { this.name = name; this.servTime = servTime; this.addTime = System.currentTimeMillis(); } public Task(String name, int servTime,int level) { this.name = name; this.servTime = servTime; this.level = level; this.addTime = System.currentTimeMillis(); } public void execute() { try { // !重点:执行时睡眠,表示该任务耗时servTime毫秒 Thread.currentThread().sleep(servTime); } catch (InterruptedException e) { e.printStackTrace(); } System.out.println( String.format("execute:name=%s,level=%s,addTime=%s,servTime=%s", name,level, addTime, servTime)); } }
依然使用TreeMap实现排序,注意的是,key要取优先级
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 package com.itheima.schedule; import java.util.Map; import java.util.Random; import java.util.TreeMap; public class HPF { public static void main(String[] args) throws InterruptedException { //有序Map,将服务优先级作为key排序 final TreeMap<Integer, Task> treeMap = new TreeMap(); //向队列中放入5个任务 for (int i = 0; i < 5; i++) { System.out.println("add task:" + i); int servTime = new Random().nextInt(1000); //注意放入的key,是优先级,这里用i标识 treeMap.put(i, new Task("task" + i, servTime,i)); } //服务线程,任务由该线程获取和执行 new Thread(new Runnable() { @Override public void run() { while (true) { try { //有序Map中,优先级最高的,在底部部,那么自然就会优先被取出 Map.Entry<Integer, Task> entry = treeMap.pollLastEntry(); if (entry == null) { Thread.currentThread().sleep(100); } else { entry.getValue().execute(); } } catch (Exception e) { e.printStackTrace(); } } } }).start(); } }
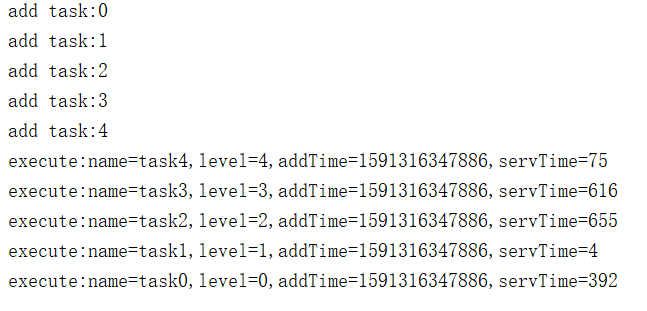
3)结果分析
按0-4顺序加入task
执行时,按4-0,优先级高的先得到执行,而与服务时间,加入的时间无关
4.5 应用案例
CPU资源调度
云计算资源调度
容器化Docker编排与调度
5定时算法与应用 系统或者项目中难免会遇到各种需要自动去执行的任务,实现这些任务的手段也多种多样,如操作系统的crontab,spring框架的quartz,java的Timer和ScheduledThreadPool都是定时任务中的典型手段。
5.1 最小堆 1)概述
Timer是java中最典型的基于优先级队列+最小堆实现的定时器,内部维护一个存放定时任务的优先级队列,该优先级队列使用了最小堆排序。当我们调用schedule方法的时候,一个新的任务被加入queue,堆重排,始终保持堆顶是执行时间最小(即最近马上要执行)的。同时,内部相当于起了一个线程不断扫描队列,从队列中依次获取堆顶元素执行,任务得到调度。
下面以Timer为例,介绍优先级队列+最小堆算法的实现原理:
2)案例
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 package com.itheima.timer; import java.util.Timer; import java.util.TimerTask; class Task extends TimerTask { @Override public void run() { System.out.println("running..."); } } public class TimerDemo { public static void main(String[] args) { Timer t=new Timer(); //在1秒后执行,以后每2秒跑一次 t.schedule(new Task(), 1000,2000); } }
3)源码分析
新加任务时,t.schedule方法会add到队列
1 2 3 4 5 6 7 8 void add(TimerTask task) { // Grow backing store if necessary if (size + 1 == queue.length) queue = Arrays.copyOf(queue, 2*queue.length); queue[++size] = task; fixUp(size); }
add实现了容量维护,不足时扩容,同时将新任务追加到队列队尾,触发堆排序,始终保持堆顶元素最小
1 2 3 4 5 6 7 8 9 10 11 12 13 14 //最小堆排序 private void fixUp(int k) { while (k > 1) { //k指针指向当前新加入的节点,也就是队列的末尾节点,j为其父节点 int j = k >> 1; //如果新加入的执行时间比父节点晚,那不需要动 if (queue[j].nextExecutionTime <= queue[k].nextExecutionTime) break; //如果大于其父节点,父子交换 TimerTask tmp = queue[j]; queue[j] = queue[k]; queue[k] = tmp; //交换后,当前指针继续指向新加入的节点,继续循环,知道堆重排合格 k = j; } }
线程调度中的run,主要调用内部mainLoop()方法,使用while循环
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 private void mainLoop() { while (true) { try { TimerTask task; boolean taskFired; synchronized(queue) { //... // Queue nonempty; look at first evt and do the right thing long currentTime, executionTime; task = queue.getMin(); synchronized(task.lock) { //... //当前时间 currentTime = System.currentTimeMillis(); //要执行的时间 executionTime = task.nextExecutionTime; //判断是否到了执行时间 if (taskFired = (executionTime<=currentTime)) { //判断下一次执行时间,单次的执行完移除 //循环的修改下次执行时间 if (task.period == 0) { // Non-repeating, remove queue.removeMin(); task.state = TimerTask.EXECUTED; } else { // Repeating task, reschedule //下次时间的计算有两种策略 //1.period是负数,那下一次的执行时间就是当前时间-period //2.period是正数,那下一次就是该任务本次的执行时间+period //注意!这两种策略大不相同。因为Timer是单线程的 //如果是1,那么currentTime是当前时间,就受任务执行长短影响 //如果是2,那么executionTime是绝对时间戳,与任务长短无关 queue.rescheduleMin( task.period<0 ? currentTime - task.period : executionTime + task.period); } } } //不到执行时间,等待 if (!taskFired) // Task hasn't yet fired; wait queue.wait(executionTime - currentTime); } //到达执行时间,run! if (taskFired) // Task fired; run it, holding no locks task.run(); } catch(InterruptedException e) { } } }
4)应用
本节使用Timer为了介绍算法原理,但是Timer已过时,实际应用中推荐使用ScheduledThreadPoolExecutor(同样内部使用DelayedWorkQueue和最小堆排序)
Timer是单线程,一旦一个失败或出现异常,将打断全部任务队列,线程池不会
Timer在jdk1.3+,而线程池需要jdk1.5+
5.2 时间轮 1)概述
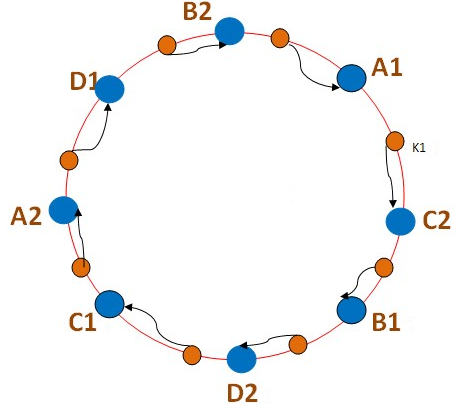
时间轮是一种更为常见的定时调度算法,各种操作系统的定时任务调度,linux crontab,基于java的通信框架Netty等。其灵感来源于我们生活中的时钟。
轮盘实际上是一个头尾相接的环状数组,数组的个数即是插槽数,每个插槽中可以放置任务。
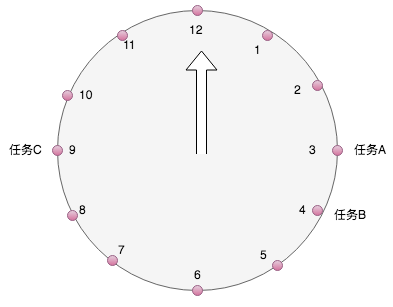
以1天为例,将任务的执行时间%12,根据得到的数值,放置在时间轮上,小时指针沿着轮盘扫描,扫到的点取出任务执行:
答案:在每个槽上设置一个队列,队列可以无限追加,解决时间点冲突问题(类似HashMap结构)
问题:每个轮盘的时间有限,比如1个月后的第3天的5点怎么办?
方案一:加长时间刻度,扩充到1年
优缺点:简单,占据大量内存,即使插槽没有任务也要空轮询,白白的资源浪费,时间、空间复杂度都高
方案二:每个任务记录一个计数器,表示转多少圈后才会执行。没当指针过来后,计数器减1,减到0的再执行
优缺点:每到一个指针都需要取出链表遍历判断,时间复杂度高,但是空间复杂度低
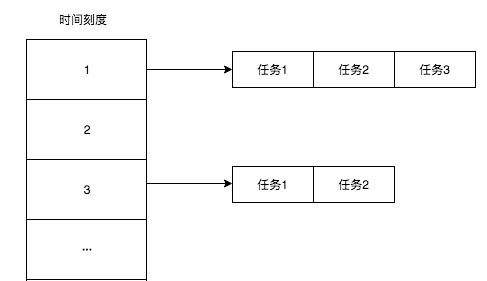
方案三:设置多个时间轮,年轮,月轮,天轮。1天内的放入天轮,1年后的则放入年轮,当年轮指针读到后,将任务取出,放入下一级的月轮对应的插槽,月轮再到天轮,直到最小精度取到,任务被执行。
优缺点:不需要额外的遍历时间,但是占据了多个轮的空间。空间复杂度升高,但是时间复杂度降低
2)java实现
定义Task类
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 package com.itheima.timer; public class RoundTask { //延迟多少秒后执行 int delay; //加入的序列号,只是标记一下加入的顺序 int index; public RoundTask(int index, int delay) { this.index = index; this.delay = delay; } void run() { System.out.println("task " + index + " start , delay = "+delay); } @Override public String toString() { return String.valueOf(index+"="+delay); } }
时间轮算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 package com.itheima.timer; import java.util.LinkedList; import java.util.Random; import java.util.concurrent.Executors; import java.util.concurrent.ScheduledExecutorService; import java.util.concurrent.TimeUnit; import java.util.concurrent.atomic.AtomicInteger; public class RoundDemo { //小轮槽数 int size1=10; //大轮槽数 int size2=5; //小轮,数组,每个元素是一个链表 LinkedList<RoundTask>[] t1 = new LinkedList[size1]; //大轮 LinkedList<RoundTask>[] t2 = new LinkedList[size2]; //小轮计数器,指针跳动的格数,每秒加1 final AtomicInteger flag1=new AtomicInteger(0); //大轮计数器,指针跳动个格数,即每10s加1 final AtomicInteger flag2=new AtomicInteger(0); //调度器,拖动指针跳动 ScheduledExecutorService service = Executors.newScheduledThreadPool(2); public RoundDemo(){ //初始化时间轮 for (int i = 0; i < size1; i++) { t1[i]=new LinkedList<>(); } for (int i = 0; i < size2; i++) { t2[i]=new LinkedList<>(); } } //打印时间轮的结构,数组+链表 void print(){ System.out.println("t1:"); for (int i = 0; i < t1.length; i++) { System.out.println(t1[i]); } System.out.println("t2:"); for (int i = 0; i < t2.length; i++) { System.out.println(t2[i]); } } //添加任务到时间轮 void add(RoundTask task){ int delay = task.delay; if (delay < size1){ //10以内的,在小轮 t1[delay].addLast(task); }else { //超过小轮的放入大轮,槽除以小轮的长度 t2[delay/size1].addLast(task); } } void startT1(){ //每秒执行一次,推动时间轮旋转,取到任务立马执行 service.scheduleAtFixedRate(new Runnable() { @Override public void run() { int point = flag1.getAndIncrement()%size1; System.out.println("t1 -----> slot "+point); LinkedList<RoundTask> list = t1[point]; if (!list.isEmpty()){ //如果当前槽内有任务,取出来,依次执行,执行完移除 while (list.size() != 0){ list.getFirst().run(); list.removeFirst(); } } } },0,1, TimeUnit.SECONDS); } void startT2(){ //每10秒执行一次,推动时间轮旋转,取到任务下方到t1 service.scheduleAtFixedRate(new Runnable() { @Override public void run() { int point = flag2.getAndIncrement()%size2; System.out.println("t2 =====> slot "+point); LinkedList<RoundTask> list = t2[point]; if (!list.isEmpty()){ //如果当前槽内有任务,取出,放到定义的小轮 while (list.size() != 0){ RoundTask task = list.getFirst(); //放入小轮哪个槽呢?小轮的槽按10取余数 t1[task.delay % size1].addLast(task); //从大轮中移除 list.removeFirst(); } } } },0,10, TimeUnit.SECONDS); } public static void main(String[] args) { RoundDemo roundDemo = new RoundDemo(); //生成100个任务,每个任务的延迟时间随机 for (int i = 0; i < 100; i++) { roundDemo.add(new RoundTask(i,new Random().nextInt(50))); } //打印,查看时间轮任务布局 roundDemo.print(); //启动大轮 roundDemo.startT2(); //小轮启动 roundDemo.startT1(); } }
3)结果分析
输出结果严格按delay顺序执行,而不管index是何时被提交的
t1为小轮,10个槽,每个1s,10s一轮回
t2为大轮,5个槽,每个10s,50s一轮回
t1循环到每个槽时,打印槽内的任务数据,如 t1–>slot9 , 打印了3个9s执行的数据
t2循环到每个槽时,将槽内的任务delay时间取余10后,放入对应的t1槽中,如 t2==>slot1
那么t1旋转对应的圈数后,可以取到t2下放过来的任务并执行,如10,11….
6 负载均衡算法 负载均衡,英文名称为Load Balance,其含义就是指将负载(工作任务)进行平衡、分摊到多个操作单元上进行运行,例如FTP服务器、Web服务器、企业核心应用服务器和其它主要任务服务器等,从而协同完成工作任务。既然涉及到多个机器,就涉及到任务如何分发,这就是负载均衡算法问题。
6.1 轮询(RR) - 【拓展】 1)概述
轮询即排好队,一个接一个。前面调度算法中用到的时间片轮转,就是一种典型的轮询。但是前面使用数组和下标轮询实现。这里尝试手动写一个双向链表形式实现服务器列表的请求轮询算法。
2)实现
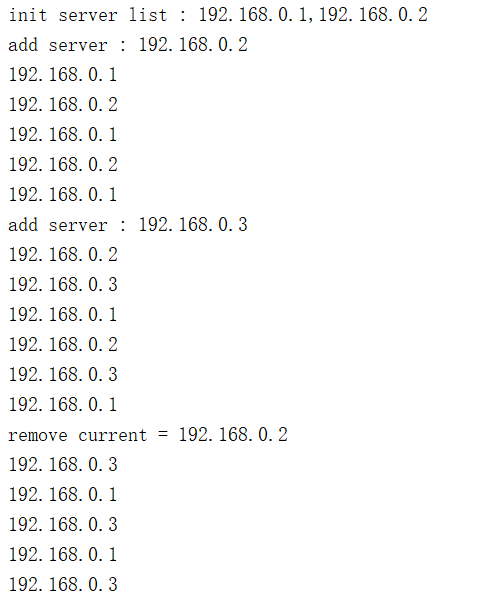
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 package com.itheima.balance; public class RR { class Server{ Server prev; Server next; String name; public Server(String name){ this.name = name; } } //当前服务节点 Server current; //初始化轮询类,多个服务器ip用逗号隔开 public RR(String serverName){ System.out.println("init server list : "+serverName); String[] names = serverName.split(","); for (int i = 0; i < names.length; i++) { Server server = new Server(names[i]); if (current == null){ //如果当前服务器为空,说明是第一台机器,current就指向新创建的server this.current = server; //同时,server的前后均指向自己。 current.prev = current; current.next = current; }else { //否则说明已经有机器了,按新加处理。 addServer(names[i]); } } } //添加机器 void addServer(String serverName){ System.out.println("add server : "+serverName); Server server = new Server(serverName); Server next = this.current.next; //在当前节点后插入新节点 this.current.next = server; server.prev = this.current; //修改下一节点的prev指针 server.next = next; next.prev=server; } //将当前服务器移除,同时修改前后节点的指针,让其直接关联 //移除的current会被回收器回收掉 void remove(){ System.out.println("remove current = "+current.name); this.current.prev.next = this.current.next; this.current.next.prev = this.current.prev; this.current = current.next; } //请求。由当前节点处理即可 //注意:处理完成后,current指针后移 void request(){ System.out.println(this.current.name); this.current = current.next; } public static void main(String[] args) throws InterruptedException { //初始化两台机器 RR rr = new RR("192.168.0.1,192.168.0.2"); //启动一个额外线程,模拟不停的请求 new Thread(new Runnable() { @Override public void run() { while (true) { try { Thread.sleep(500); } catch (InterruptedException e) { e.printStackTrace(); } rr.request(); } } }).start(); //3s后,3号机器加入清单 Thread.currentThread().sleep(3000); rr.addServer("192.168.0.3"); //3s后,当前服务节点被移除 Thread.currentThread().sleep(3000); rr.remove(); } }
3)结果分析
初始化后,只有1,2,两者轮询
3加入后,1,2,3,三者轮询
移除2后,只剩1和3轮询
4)优缺点
实现简单,机器列表可以自由加减,且时间复杂度为o(1)
无法针对节点做偏向性定制,节点处理能力的强弱无法区分对待
6.2 随机(Random) 1)概述
从可服务的列表中随机取一个提供响应。随机存取的场景下,适合使用数组更高效的实现下标随机读取。
2)实现
定义一个数组,在数组长度内取随机数,作为其下标即可。非常简单
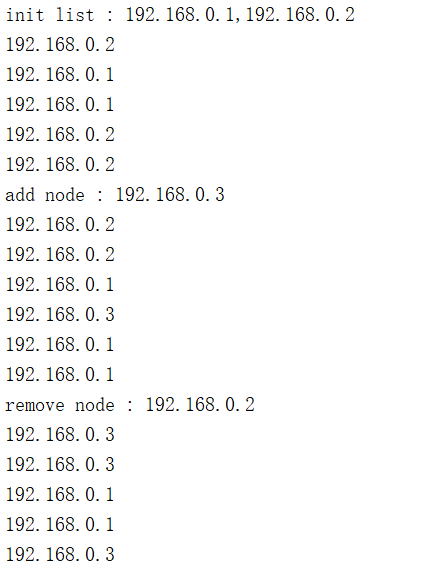
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 package com.itheima.balance; import java.util.ArrayList; import java.util.Random; public class Rand { ArrayList<String> ips ; public Rand(String nodeNames){ System.out.println("init list : "+nodeNames); String[] nodes = nodeNames.split(","); //初始化服务器列表,长度取机器数 ips = new ArrayList<>(nodes.length); for (String node : nodes) { ips.add(node); } } //请求 void request(){ //下标,随机数,注意因子 int i = new Random().nextInt(ips.size()); System.out.println(ips.get(i)); } //添加节点,注意,添加节点会造成内部数组扩容 //可以根据实际情况初始化时预留一定空间 void addnode(String nodeName){ System.out.println("add node : "+nodeName); ips.add(nodeName); } //移除 void remove(String nodeName){ System.out.println("remove node : "+nodeName); ips.remove(nodeName); } public static void main(String[] args) throws InterruptedException { Rand rd = new Rand("192.168.0.1,192.168.0.2"); //启动一个额外线程,模拟不停的请求 new Thread(new Runnable() { @Override public void run() { while (true) { try { Thread.sleep(500); } catch (InterruptedException e) { e.printStackTrace(); } rd.request(); } } }).start(); //3s后,3号机器加入清单 Thread.currentThread().sleep(3000); rd.addnode("192.168.0.3"); //3s后,当前服务节点被移除 Thread.currentThread().sleep(3000); rd.remove("192.168.0.2"); } }
3)结果分析
初始化为1,2,两者不按顺序轮询,而是随机出现
3加入服务节点列表
移除2后,只剩1,3,依然是两者随机,无序
6.3 源地址哈希(Hash) 1)概述
对当前访问的ip地址做一个hash值,相同的key被路由到同一台机器去。场景常见于分布式集群环境下,用户登录时的请求路由和会话保持。
2)实现
使用HashMap可以实现请求值到对应节点的服务,其查找时的时间复杂度为o(1)。固定一种算法,将请求映射到key上即可。举例,将请求的来源ip末尾,按机器数取余作为key:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 package com.itheima.balance; import java.util.ArrayList; import java.util.Random; public class Hash { ArrayList<String> ips ; public Hash(String nodeNames){ System.out.println("init list : "+nodeNames); String[] nodes = nodeNames.split(","); //初始化服务器列表,长度取机器数 ips = new ArrayList<>(nodes.length); for (String node : nodes) { ips.add(node); } } //添加节点,注意,添加节点会造成内部Hash重排,思考为什么呢??? //这是个问题!在一致性hash中会进入详细探讨 void addnode(String nodeName){ System.out.println("add node : "+nodeName); ips.add(nodeName); } //移除 void remove(String nodeName){ System.out.println("remove node : "+nodeName); ips.remove(nodeName); } //映射到key的算法,这里取余数做下标 private int hash(String ip){ int last = Integer.valueOf(ip.substring(ip.lastIndexOf(".")+1,ip.length())); return last % ips.size(); } //请求 //注意,这里和来访ip是有关系的,采用一个参数,表示当前的来访ip void request(String ip){ //下标 int i = hash(ip); System.out.println(ip+"-->"+ips.get(i)); } public static void main(String[] args) { Hash hash = new Hash("192.168.0.1,192.168.0.2"); for (int i = 1; i < 10; i++) { //模拟请求的来源ip String ip = "192.168.1."+ i; hash.request(ip); } hash.addnode("192.168.0.3"); for (int i = 1; i < 10; i++) { //模拟请求的来源ip String ip = "192.168.1."+ i; hash.request(ip); } } }
3)结果分析
初始化后,只有1,2,下标为末尾ip取余数,多次运行,响应的机器不变,实现了会话保持
3加入后,重新hash,机器分布发生变化
2被移除后,原来hash到2的请求被重新定位给3响应
6.4 加权轮询(WRR) 1)概述
WeightRoundRobin,轮询只是机械的旋转,加权轮询弥补了所有机器一视同仁的缺点。在轮询的基础上,初始化时,机器携带一个比重。
2)实现
维护一个链表,每个机器根据权重不同,占据的个数不同。轮询时权重大的,个数多,自然取到的次数变大。举个例子:a,b,c 三台机器,权重分别为4,2,1,排位后会是a,a,a,a,b,b,c,每次请求时,从列表中依次取节点,下次请求再取下一个。到末尾时,再从头开始。
但是这样有一个问题:机器分布不够均匀,扎堆出现了….
解决:为解决机器平滑出现的问题,nginx的源码中使用了一种平滑的加权轮询的算法,规则如下:
每个节点两个权重,weight和currentWeight,weight永远不变是配置时的值,current不停变化
变化规律如下:选择前所有current+=weight,选current最大的响应,响应后让它的current-=total
次数
响应前
被选中
响应后
1
4,2,1
a
-3,2,1
2
1,4,2
b
1,-3,2
3
5,-1,3
a
-2,-1,3
4
2,1,4
c
2,1,-3
5
6,3,-2
a
-1,3,-2
6
3,5,-1
b
3,-2,-1
7
7,0,0
a
0,0,0
统计:a=4,b=2,c=1 且分布平滑均衡
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 package com.itheima.balance; import java.util.ArrayList; public class WRR { class Node{ int weight,currentWeight; String name; public Node(String name,int weight){ this.name = name; this.weight = weight; this.currentWeight = 0; } @Override public String toString() { return String.valueOf(currentWeight); } } //所有节点的列表 ArrayList<Node> list ; //总权重 int total; //初始化节点列表,格式:a#4,b#2,c#1 public WRR(String nodes){ String[] ns = nodes.split(","); list = new ArrayList<>(ns.length); for (String n : ns) { String[] n1 = n.split("#"); int weight = Integer.valueOf(n1[1]); list.add(new Node(n1[0],weight)); total += weight; } } //获取当前节点 Node getCurrent(){ //执行前,current加权重 for (Node node : list) { node.currentWeight += node.weight; } //遍历,取权重最高的返回 Node current = list.get(0); int i = 0; for (Node node : list) { if (node.currentWeight > i){ i = node.currentWeight; current = node; } } return current; } //响应 void request(){ //获取当前节点 Node node = this.getCurrent(); //第一列,执行前的current System.out.print(list.toString()+"---"); //第二列,选中的节点开始响应 System.out.print(node.name+"---"); //响应后,current减掉total node.currentWeight -= total; //第三列,执行后的current System.out.println(list); } public static void main(String[] args) { WRR wrr = new WRR("a#4,b#2,c#1"); //7次执行请求,看结果 for (int i = 0; i < 7; i++) { wrr.request(); } } }
3)结果分析
6.5 加权随机(WR) 1)概述
WeightRandom,机器随机被筛选,但是做一组加权值,根据权值不同,选中的概率不同。在这个概念上,可以认为随机是一种等权值的特殊情况。
2)实现
设计思路依然相同,根据权值大小,生成不同数量的节点,节点排队后,随机获取。这里的数据结构主要涉及到随机的读取,所以优选为数组。
与随机相同的是,同样为数组随机筛选,不同在于,随机只是每台机器1个,加权后变为多个。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 package com.itheima.balance; import java.util.ArrayList; import java.util.Random; public class WR { //所有节点的列表 ArrayList<String> list ; //初始化节点列表 public WR(String nodes){ String[] ns = nodes.split(","); list = new ArrayList<>(); for (String n : ns) { String[] n1 = n.split("#"); int weight = Integer.valueOf(n1[1]); for (int i = 0; i < weight; i++) { list.add(n1[0]); } } } void request(){ //下标,随机数,注意因子 int i = new Random().nextInt(list.size()); System.out.println(list.get(i)); } public static void main(String[] args) { WR wr = new WR("a#2,b#1"); for (int i = 0; i < 9; i++) { wr.request(); } } }
3)结果分析
运行9次,a,b交替出现,a=6,b=3,满足2:1比例
注意!既然是随机,就存在随机性,不见得每次执行都会严格比例。样本趋向无穷时,比例约准确
6.6 最小连接数(LC) - 【拓展】 1)概述
LeastConnections,即统计当前机器的连接数,选最少的去响应新的请求。前面的算法是站在请求维度,而最小连接数是站在机器的维度。
2)实现
定义一个链接表记录机器的节点id和机器连接数量的计数器。内部采用最小堆做排序处理,响应时取堆顶节点即是最小连接数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 package com.itheima.balance; import java.util.Arrays; import java.util.Random; import java.util.concurrent.atomic.AtomicInteger; public class LC { //节点列表 Node[] nodes; //初始化节点,创建堆 // 因为开始时各节点连接数都为0,所以直接填充数组即可 LC(String ns){ String[] ns1 = ns.split(","); nodes = new Node[ns1.length+1]; for (int i = 0; i < ns1.length; i++) { nodes[i+1] = new Node(ns1[i]); } } //节点下沉,与左右子节点比对,选里面最小的交换 //目的是始终保持最小堆的顶点元素值最小 //i:要下沉的顶点序号 void down(int i) { //顶点序号遍历,只要到1半即可,时间复杂度为O(log2n) while ( i << 1 < nodes.length){ //左子,为何左移1位?回顾一下二叉树序号 int left = i<<1; //右子,左+1即可 int right = left+1; //标记,指向 本节点,左、右子节点里最小的,一开始取i自己 int flag = i; //判断左子是否小于本节点 if (nodes[left].get() < nodes[i].get()){ flag = left; } //判断右子 if (right < nodes.length && nodes[flag].get() > nodes[right].get()){ flag = right; } //两者中最小的与本节点不相等,则交换 if (flag != i){ Node temp = nodes[i]; nodes[i] = nodes[flag]; nodes[flag] = temp; i = flag; }else { //否则相等,堆排序完成,退出循环即可 break; } } } //请求。非常简单,直接取最小堆的堆顶元素就是连接数最少的机器 void request(){ System.out.println("---------------------"); //取堆顶元素响应请求 Node node = nodes[1]; System.out.println(node.name + " accept"); //连接数加1 node.inc(); //排序前的堆 System.out.println("before:"+Arrays.toString(nodes)); //堆顶下沉 down(1); //排序后的堆 System.out.println("after:"+Arrays.toString(nodes)); } public static void main(String[] args) { //假设有7台机器 LC lc = new LC("a,b,c,d,e,f,g"); //模拟10个请求连接 for (int i = 0; i < 10; i++) { lc.request(); } } class Node{ //节点标识 String name; //计数器 AtomicInteger count = new AtomicInteger(0); public Node(String name){ this.name = name; } //计数器增加 public void inc(){ count.getAndIncrement(); } //获取连接数 public int get(){ return count.get(); } @Override public String toString() { return name+"="+count; } } }
3)结果分析
初始化后,堆节点值都为0,即每个机器连接数都为0
堆顶连接后,下沉,堆重新排序,最小堆规则保持成立
6.7 应用案例 1)nginx upstream
1 2 3 4 5 6 7 8 9 upstream frontend { #源地址hash ip_hash; server 192.168.0.1:8081; server 192.168.0.2:8082 weight=1 down; server 192.168.0.3:8083 weight=2; server 192.168.0.4:8084 weight=3 backup; server 192.168.0.5:8085 weight=4 max_fails=3 fail_timeout=30s; }
ip_hash:即源地址hash算法
down:表示当前的server暂时不参与负载
weight:即加权算法,默认为1,weight越大,负载的权重就越大。
backup:备份机器,只有其它所有的非backup机器down或者忙的时候,再请求backup机器。
max_fails:最大失败次数,默认值为1,这里为3,也就是最多进行3次尝试
fail_timeout:超时时间为30秒,默认值是10s。
注意!weight和backup不能和ip_hash关键字一起使用。
2)springcloud ribbon IRule
1 2 #设置负载均衡策略 eureka-application-service为调用的服务的名称 eureka-application-service.ribbon.NFLoadBalancerRuleClassName=com.netflix.loadbalancer.RandomRule
RoundRobinRule:轮询
RandomRule:随机
AvailabilityFilteringRule:先过滤掉由于多次访问故障而处于断路器跳闸状态的服务,还有并发的连接数量超过阈值的服务,然后对剩余的服务轮询
WeightedResponseTimeRule:根据平均响应时间计算所有服务的权重,响应时间越快服务权重越大。刚启动时如果统计信息不足,则使用RoundRobinRule策略,等统计信息足够,会切换到该策略
RetryRule:先按照RoundRobinRule的策略,如果获取服务失败则在指定时间内重试,获取可用的服务
BestAvailableRule:会先过滤掉由于多次访问故障而处于断路器跳闸状态的服务,然后选择一个并发量最小的服务
ZoneAvoidanceRule:默认规则,综合判断server所在区域的性能和server的可用性
3)dubbo负载均衡
使用Service注解
1 @Service(loadbalance = "roundrobin",weight = 100)
RandomLoadBalance: 随机,这种方式是dubbo默认的负载均衡策略
RoundRobinLoadBalance:轮询
LeastActiveLoadBalance:最少活跃次数,dubbo框架自定义了一个Filter,用于计算服务被调用的次数
ConsistentHashLoadBalance:一致性hash
7 加密算法的应用 - 【拓展】 7.1 散列 1)概述
严格来讲这不算是一种加密,而应该叫做信息摘要算法。该算法使用散列函数把消息或数据压缩成摘要,使得数据量变小,将数据的格式固定下来。通过数据打乱混合,重新创建一个叫做 散列值
2)常见算法
MD5、SHA(128、256)系列
3)应用
常用于密码存储,或文件指纹校验。
网站用户注册后,密码经过MD5加密后的值,存储进DB。再次登录时,将用户输入的密码按同样的方式加密,与数据库中的密文比对。这样即使数据库被破解,或者开发人员可见,基于MD5的不可逆性,仍然不知道密码是什么。
其次是文件校验场景。例如从某站下载的文件(尤其是大文件,比如系统镜像iso),官方网站都会放置一个签名(可能是MD5,或者SHA),当用户拿到文件后,可以本地执行散列算法与官网签名比对是否一致,来判断文件是否被篡改。如ubuntu20.04的镜像:
4)实现
先添加commons坐标
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 <dependency> <groupId>commons-codec</groupId> <artifactId>commons-codec</artifactId> <version>1.14</version> </dependency> package com.itheima.pwd; import org.apache.commons.codec.digest.DigestUtils; import java.math.BigInteger; import java.security.MessageDigest; import java.security.NoSuchAlgorithmException; public class Hash { /** * jdk的security实现md5 * 也可以借助commons-codec包 */ public static String md5(String src) { byte[] pwd = null; try { pwd = MessageDigest.getInstance("md5").digest(src.getBytes("utf-8")); } catch (Exception e) { e.printStackTrace(); } String code = new BigInteger(1, pwd).toString(16); for (int i = 0; i < 32 - code.length(); i++) { code = "0" + code; } return code; } public static String commonsMd5(String src){ return DigestUtils.md5Hex(src); } /** * jdk实现sha算法 * 也可以借助commons-codec包 */ public static String sha(String src) throws Exception { MessageDigest sha = MessageDigest.getInstance("sha"); byte[] shaByte = sha.digest(src.getBytes("utf-8")); StringBuffer code = new StringBuffer(); for (int i = 0; i < shaByte.length; i++) { int val = ((int) shaByte[i]) & 0xff; if (val < 16) { code.append("0"); } code.append(Integer.toHexString(val)); } return code.toString(); } public static String commonsSha(String src) throws Exception { return DigestUtils.sha1Hex(src); } public static void main(String[] args) throws Exception { String name = "架构师训练营"; System.out.println(name); System.out.println(md5(name)); System.out.println(commonsMd5(name)); System.out.println(sha(name)); System.out.println(commonsSha(name)); } }
5)结果分析
jdk与commons均生成了相同的散列值
多次运行,依然生成固定值
commons-codec还有很多可用方法,如:sha256,sha512…
7.2 对称 1)概述
加密与解密用的都是同一个秘钥,性能比非对称加密高很多。
2)常见算法
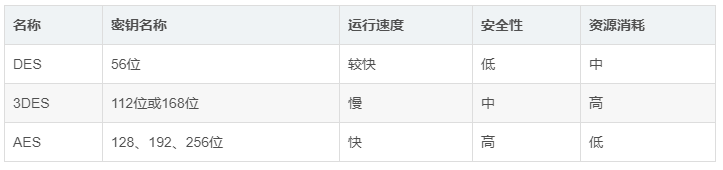
常见的对称加密算法有 DES、3DES、AES
DES算法在POS、ATM、磁卡及智能卡(IC卡)、加油站、高速公路收费站等领域被广泛应用,以此来实现关键数据的保密,如信用卡持卡人的PIN的加密传输,IC卡与POS间的双向认证、金融交易数据包的MAC校验等
3DES是DES加密算法的一种模式,是DES的一个更安全的变形。从DES向AES的过渡算法
AES,是下一代的加密算法标准,速度快,安全级别更高。
3)应用
常用于对效率要求较高的实时数据加密通信。
4)实现
以AES为例:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 package com.itheima.pwd; import org.apache.commons.codec.binary.Base64; import javax.crypto.Cipher; import javax.crypto.KeyGenerator; import javax.crypto.SecretKey; import javax.crypto.spec.SecretKeySpec; import java.security.Key; import java.security.NoSuchAlgorithmException; public class AES { public static void main(String[] args) throws Exception { //生成KEY KeyGenerator keyGenerator = KeyGenerator.getInstance("AES"); keyGenerator.init(128); //key转换 Key key = new SecretKeySpec(keyGenerator.generateKey().getEncoded(), "AES"); Cipher cipher = Cipher.getInstance("AES/ECB/PKCS5Padding"); String src = "架构师训练营"; System.out.println("明文:"+src); //加密 cipher.init(Cipher.ENCRYPT_MODE, key); byte[] result = cipher.doFinal(src.getBytes()); System.out.println("加密:" + Base64.encodeBase64String(result)); //解密 cipher.init(Cipher.DECRYPT_MODE, key); result = cipher.doFinal(result); System.out.println("解密:" + new String(result)); } }
5)结果分析
7.3 非对称 1)概述
非对称即加密与解密不是同一把钥匙,而是分成公钥和私钥。私钥在个人手里,公钥公开。这一对钥匙一个用于加密,另一个用于解密。使用其中一个加密后,则原始明文只能用对应的另一个密钥解密,即使最初用于加密的密钥也不能用作解密。正是因为这种特性,所以称为非对称加密。
2)常见算法
RSA、ElGamal、背包算法、Rabin(RSA的特例)、迪菲-赫尔曼密钥交换协议中的公钥加密算法、椭圆曲线加密算法(英语:Elliptic Curve Cryptography, ECC)。使用最广泛的是RSA算法(发明者Rivest、Shmir和Adleman姓氏首字母缩写)
3)应用
最常见的,两点:https和数字签名。
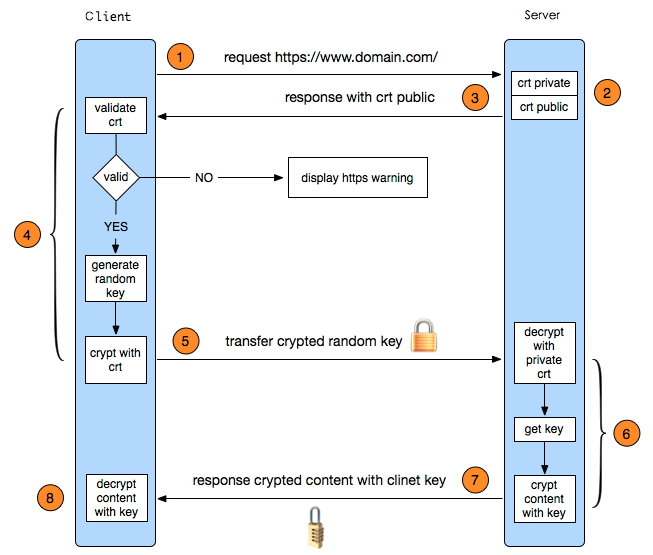
严格意义上讲,https并非所有请求都使用非对称。基于性能考虑,https先使用非对称约定一个key,后期使用该key进行对称加密和数据传输。
数字签名则是用于验证报文是否为服务器发出的,用于防伪和认证。过程如下:
签发:
服务器外发布公钥,私钥保密
服务器对消息M计算摘要(如MD5等公开算法),得到摘要D
服务器使用私钥对D进行签名,得到签名S
将M和S一起发给客户
验证:
客户端对M使用同一摘要算法计算摘要,得到摘要D
使用服务器公钥对S进行解密,得到摘要D’
如果D和D’相同,那么证明M确实是服务器发出的
4)实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 package com.itheima.pwd; import org.apache.commons.codec.binary.Base64; import javax.crypto.Cipher; import java.security.*; import java.security.interfaces.RSAPrivateKey; import java.security.interfaces.RSAPublicKey; import java.security.spec.PKCS8EncodedKeySpec; import java.security.spec.X509EncodedKeySpec; public class RSAUtil { static String privKey ; static String publicKey; public static void main(String[] args) throws Exception { //生成公钥和私钥 genKeyPair(); //加密字符串 String message = "架构师训练营"; System.out.println("明文:"+message); System.out.println("随机公钥为:" + publicKey); System.out.println("随机私钥为:" + privKey); String messageEn = encrypt(message,publicKey); System.out.println("公钥加密:" + messageEn); String messageDe = decrypt(messageEn,privKey); System.out.println("私钥解密:" + messageDe); } /** * 随机生成密钥对 */ public static void genKeyPair() throws NoSuchAlgorithmException { // KeyPairGenerator类用于生成公钥和私钥对,基于RSA算法生成对象 KeyPairGenerator keyPairGen = KeyPairGenerator.getInstance("RSA"); // 初始化密钥对生成器,密钥大小为96-1024位 keyPairGen.initialize(1024,new SecureRandom()); // 生成一个密钥对,保存在keyPair中 KeyPair keyPair = keyPairGen.generateKeyPair(); privKey = new String(Base64.encodeBase64((keyPair.getPrivate().getEncoded()))); publicKey = new String(Base64.encodeBase64(keyPair.getPublic().getEncoded())); } /** * RSA公钥加密 */ public static String encrypt( String str, String publicKey ) throws Exception{ //base64编码的公钥 byte[] decoded = Base64.decodeBase64(publicKey); RSAPublicKey pubKey = (RSAPublicKey) KeyFactory.getInstance("RSA").generatePublic(new X509EncodedKeySpec(decoded)); //RSA加密 Cipher cipher = Cipher.getInstance("RSA"); cipher.init(Cipher.ENCRYPT_MODE, pubKey); String outStr = Base64.encodeBase64String(cipher.doFinal(str.getBytes("UTF-8"))); return outStr; } /** * RSA私钥解密 */ public static String decrypt(String str, String privateKey) throws Exception{ //64位解码加密后的字符串 byte[] inputByte = Base64.decodeBase64(str.getBytes("UTF-8")); byte[] decoded = Base64.decodeBase64(privateKey); RSAPrivateKey priKey = (RSAPrivateKey) KeyFactory.getInstance("RSA").generatePrivate(new PKCS8EncodedKeySpec(decoded)); Cipher cipher = Cipher.getInstance("RSA"); cipher.init(Cipher.DECRYPT_MODE, priKey); return new String(cipher.doFinal(inputByte)); } }
5)结果分析
加密解密实现完整还原
必须用另一把钥匙解密,如果用公钥加密后再使用公钥解密,则失败
8 一致性hash及其应用 8.1背景 负载均衡策略中,我们提到过源地址hash算法,让某些请求固定的落在对应的服务器上。这样可以解决会话信息保留的问题。
同时,标准的hash,如果机器节点数发生变更。那么请求会被重新hash,打破了原始的设计初衷,怎么解决呢?一致性hash上场。
8.2 原理
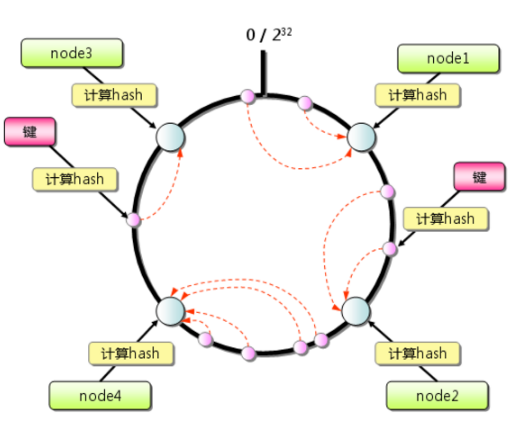
以4台机器为例,一致性hash的算法如下:
首先求出各个服务器的哈希值,并将其配置到0~232的圆上
然后采用同样的方法求出存储数据的键的哈希值,也映射圆上
从数据映射到的位置开始顺时针查找,将数据保存到找到的第一个服务器上
如果到最大值仍然找不到,就取第一个。这就是为啥形象的称之为环
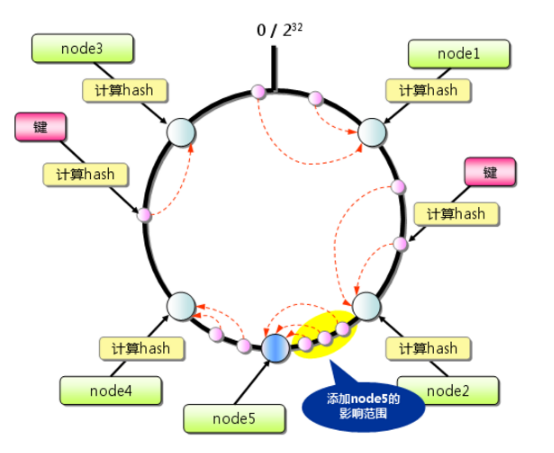
添加节点:
删除节点原理雷同
8.3 特性
单调性(Monotonicity):单调性是指如果已经有一些请求通过哈希分派到了相应的服务器进行处理,又有新的服务器加入到系统中时候,应保证原有的请求可以被映射到原有的或者新的服务器中去,而不会被映射到原来的其它服务器上去。
分散性(Spread):分布式环境中,客户端请求时可能只知道其中一部分服务器,那么两个客户端看到不同的部分,并且认为自己看到的都是完整的hash环,那么问题来了,相同的key可能被路由到不同服务器上去。以上图为例,加入client1看到的是1,4;client2看到的是2,3;那么2-4之间的key会被俩客户端重复映射到3,4上去。分散性反应的是这种问题的严重程度。
平衡性(Balance):平衡性是指客户端hash后的请求应该能够分散到不同的服务器上去。一致性hash可以做到尽量分散,但是不能保证每个服务器处理的请求的数量完全相同。这种偏差称为hash倾斜。如果节点的分布算法设计不合理,那么平衡性就会收到很大的影响。
4)优化
增加虚拟节点可以优化hash算法,使得切段和分布更细化。即实际有m台机器,但是扩充n倍,在环上放置m*n个,那么均分后,key的段会分布更细化。
8.4 实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 package com.itheima.hash; import java.util.Random; import java.util.SortedMap; import java.util.TreeMap; /** * 一致性Hash算法 */ public class Hash { //服务器列表 private static String[] servers = { "192.168.0.1", "192.168.0.2", "192.168.0.3", "192.168.0.4" }; //key表示服务器的hash值,value表示服务器 private static SortedMap<Integer, String> serverMap = new TreeMap<Integer, String>(); static { for (int i=0; i<servers.length; i++) { int hash = getHash(servers[i]); //理论上,hash环的最大值为2^32 //这里为做实例,将ip末尾作为上限也就是254 //那么服务器是0-4,乘以60后可以均匀分布到 0-254 的环上去 //实际的请求ip到来时,在环上查找即可 hash *= 60; System.out.println("add " + servers[i] + ", hash=" + hash); serverMap.put(hash, servers[i]); } } //查找节点 private static String getServer(String key) { int hash = getHash(key); //得到大于该Hash值的所有server SortedMap<Integer, String> subMap = serverMap.tailMap(hash); if(subMap.isEmpty()){ //如果没有比该key的hash值大的,则从第一个node开始 Integer i = serverMap.firstKey(); //返回对应的服务器 return serverMap.get(i); }else{ //第一个Key就是顺时针过去离node最近的那个结点 Integer i = subMap.firstKey(); //返回对应的服务器 return subMap.get(i); } } //运算hash值 //该函数可以自由定义,只要做到取值离散即可 //这里取ip地址的最后一节 private static int getHash(String str) { String last = str.substring(str.lastIndexOf(".")+1,str.length()); return Integer.valueOf(last); } public static void main(String[] args) { //模拟5个随机ip请求 for (int i = 1; i < 8; i++) { String ip = "192.168.1."+ i*30; System.out.println(ip +" ---> "+getServer(ip)); } //将5号服务器加到2-3之间,取中间位置,150 System.out.println("add 192.168.0.5,hash=150"); serverMap.put(150,"192.168.0.5"); //再次发起5个请求 for (int i = 1; i < 8; i++) { String ip = "192.168.1."+ i*30; System.out.println(ip +" ---> "+getServer(ip)); } } }
8.5 验证
4台机器加入hash环
模拟请求,根据hash值,准确调度到下游节点
添加节点5,key取150
再次发起请求
9 典型业务场景应用 9.1网站敏感词过滤 1)场景
敏感词、文字过滤是一个网站必不可少的功能,高效的过滤算法是非常有必要的。针对过滤首先想到的可能是这样:
方案一、使用java里的String contains,逐个遍历敏感词:
1 2 3 4 5 6 7 8 9 10 String[] s = "广告,广告词,中奖".split(","); String text = "讨厌的广告词"; boolean flag = false; for (String s1 : s) { if (text.contains(s1)){ flag = true; break; } } System.out.println(flag);
方案二、正则表达式:
1 System.out.println(text.matches(".*(广告|广告词|中奖).*"));
其实无论采取哪个方法,基本是换汤不换药。都是整体字符匹配,效率值得商榷。
那怎么办呢?DFA算法出场。
2)概述
DFA即Deterministic Finite Automaton,也就是确定有穷自动机,它是是通过event和当前的state得到下一个state,即event+state=nextstate。
对照到以上案例,查找和停止查找是动作,找没找到是状态,每一步的查找和结果决定下一步要不要继续。DFA算法在敏感词上应用的关键是构建敏感词库,如果我们把以上案例翻译成json表达如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 { "isEnd": 0, "广": { "isEnd": 0, "告": { "isEnd": 1, "词": { "isEnd": 1 } } }, "中": { "isEnd": 0, "奖": { "isEnd": 1 } } }
查找过程如下:首先把text按字拆分,逐个字查找词库的key,先从“讨”开始,没有就下一个字“厌”,直到“广”,找到就判断isEnd,如果为1,说明匹配成功包含敏感词,如果为0,那就继续匹配“告”,直到isEnd=1为止。
匹配策略上,有两种。最小和最大匹配。最小则匹配【广告】,最大则需要匹配到底【广告词】
3)java实现
先加入fastjson坐标,查看敏感词库结构要用到
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 <dependency> <groupId>com.alibaba</groupId> <artifactId>fastjson</artifactId> <version>1.2.70</version> </dependency> package com.itheima.busi; import com.alibaba.fastjson.JSON; import java.util.*; /** * 敏感词处理DFA算法 */ public class SensitiveWordUtil { //短匹配规则,如:敏感词库["广告","广告词"],语句:"我是广告词",匹配结果:我是[广告] public static final int SHORT_MATCH = 1; //长匹配规则,如:敏感词库["广告","广告词"],语句:"我是广告词",匹配结果:我是[广告词] public static final int LONG_MATCH = 2; /** * 敏感词库 */ public static HashMap sensitiveWordMap; /** * 初始化敏感词库 * words:敏感词,多个用英文逗号分隔 */ private static void initSensitiveWordMap(String words) { String[] w = words.split(","); sensitiveWordMap = new HashMap(w.length); Map nowMap; for (String key : w) { nowMap = sensitiveWordMap; for (int i = 0; i < key.length(); i++) { //转换成char型 char keyChar = key.charAt(i); //库中获取关键字 Map wordMap = (Map)nowMap.get(keyChar); //如果不存在新建一个,并加入词库 if (wordMap == null){ wordMap = new HashMap(); wordMap.put("isEnd", "0"); nowMap.put(keyChar, wordMap); } nowMap = wordMap; if (i == key.length() - 1) { //最后一个 nowMap.put("isEnd", "1"); } } } } /** * 判断文字是否包含敏感字符 * @return 若包含返回true,否则返回false */ public static boolean contains(String txt, int matchType) { for (int i = 0; i < txt.length(); i++) { int matchFlag = checkSensitiveWord(txt, i, matchType); //判断是否包含敏感字符 if (matchFlag > 0) { //大于0存在,返回true return true; } } return false; } /** * 沿着文本字符挨个往后检索文字中的敏感词 */ public static Set<String> getSensitiveWord(String txt, int matchType) { Set<String> sensitiveWordList = new HashSet<>(); for (int i = 0; i < txt.length(); i++) { //判断是否包含敏感字符 int length = checkSensitiveWord(txt, i, matchType); if (length > 0) {//存在,加入list中 sensitiveWordList.add(txt.substring(i, i + length)); //指针沿着文本往后移动敏感词的长度 //也就是一旦找到敏感词,加到列表后,越过这个词的字符,继续往下搜索 //但是必须减1,因为for循环会自增,如果不减会造成下次循环跳格而忽略字符 //这会造成严重误差 i = i + length - 1; } //如果找不到,i就老老实实一个字一个字的往后移动,作为begin进行下一轮 } return sensitiveWordList; } /** * 从第beginIndex个字符的位置,往后查找敏感词 * 如果找到,返回敏感词字符的长度,不存在返回0 * 这个长度用于找到后提取敏感词和后移指针,是个性能关注点 */ private static int checkSensitiveWord(String txt, int beginIndex, int matchType) { //敏感词结束标识位:用于敏感词只有1位的情况 boolean flag = false; //匹配到的敏感字的个数,也就是敏感词长度 int length = 0; char word; //从根Map开始查找 Map nowMap = sensitiveWordMap; for (int i = beginIndex; i < txt.length(); i++) { //被判断语句的第i个字符开始 word = txt.charAt(i); //获取指定key,并且将敏感库指针指向下级map nowMap = (Map) nowMap.get(word); if (nowMap != null) {//存在,则判断是否为最后一个 //找到相应key,匹配长度+1 length++; //如果为最后一个匹配规则,结束循环,返回匹配标识数 if ("1".equals(nowMap.get("isEnd"))) { //结束标志位为true flag = true; //短匹配,直接返回,长匹配还需继续查找 if (SHORT_MATCH == matchType) { break; } } } else { //敏感库不存在,直接中断 break; } } if (length < 2 || !flag) { //长度必须大于等于1才算是词,字的话就不必这么折腾了 length = 0; } return length; } public static void main(String[] args) { //初始化敏感词库 SensitiveWordUtil.initSensitiveWordMap("广告,广告词,中奖"); System.out.println("敏感词库结构:" + JSON.toJSONString(sensitiveWordMap)); String string = "关于中奖广告的广告词筛选"; System.out.println("被检测文本:"+string); System.out.println("待检测字数:" + string.length()); //是否含有关键字 boolean result = SensitiveWordUtil.contains(string,SensitiveWordUtil.LONG_MATCH); System.out.println("长匹配:"+result); result = SensitiveWordUtil.contains(string, SensitiveWordUtil.SHORT_MATCH); System.out.println("短匹配:"+result); //获取语句中的敏感词 Set<String> set = SensitiveWordUtil.getSensitiveWord(string,SensitiveWordUtil.LONG_MATCH); System.out.println("长匹配到:" + set); set = SensitiveWordUtil.getSensitiveWord(string, SensitiveWordUtil.SHORT_MATCH); System.out.println("短匹配到:" + set); } }
4)结果分析
敏感词结构初始化后符合预期
检测和长短匹配有结果
匹配的敏感词列表正确
9.2 最优商品topk 9.2.1 背景 topk是一个典型的业务场景,除了最优商品,包括推荐排名、积分排名所有涉及到排名前k的地方都是该算法的应用场合。
topk即得到一个集合后,筛选里面排名前k个数值。问题看似简单,但是里面的数据结构和算法体现着对解决方案性能的思索和深度挖掘。到底有几种方法,这些方案里蕴含的优化思路究竟是怎么样的?这节来讨论
9.2.2 方案 方案一:
全局排序,将集合整体排序后,取出最大的k个值就是需要的结果。
这种方案最糟糕,我只需要排名前k的元素,其他n-k个的顺序我并不关心,但是运算过程中,都得跟着做了没用的排序操作。
方案二:
局部排序,既然全局没必要,那我只取前k个,后面的就没必要理会了。
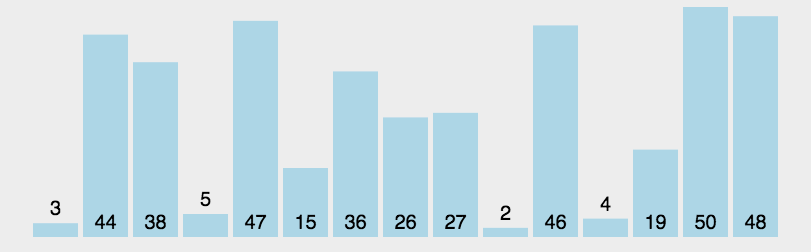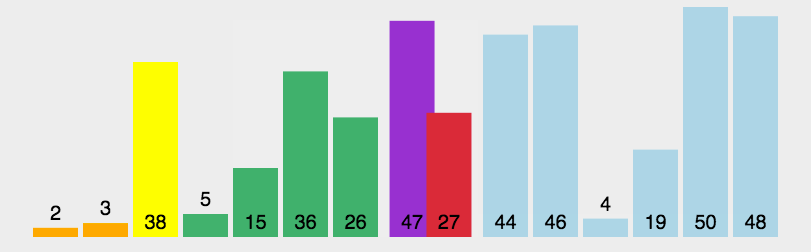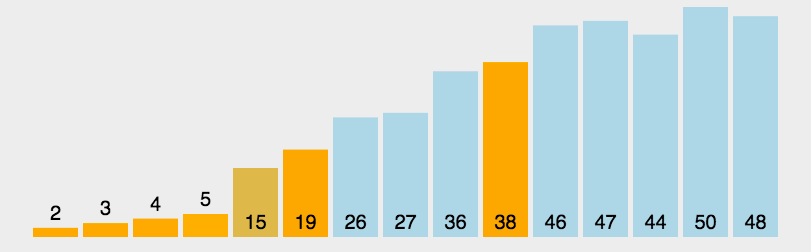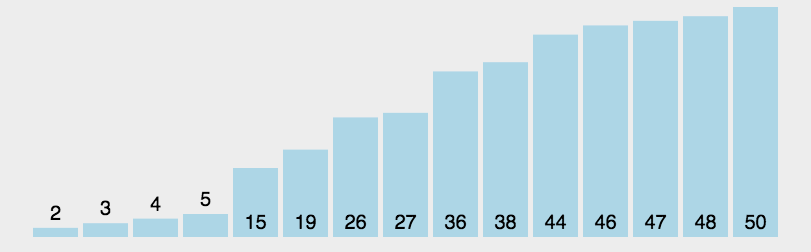
冒泡排序在排序算法中可以胜任该操作。我们按最大值往上冒泡为例,只要执行k次冒泡,那前k名就可以确定。但是这种方案依然不是最优办法。因为我们需要的是前k名,那至于这k个,谁大谁小并不需要关心,排序依然是个浪费。
方案三:
最小堆,既然没必要排序,那我们就不排序。
先将前k个元素形成一个最小堆,后面的n-k个元素依次与堆顶比较,小则丢弃大则替换堆顶并调整堆。直到n个全部完成为止。最小堆是topk的经典解决方案。
9.2.3 实现 下面就用最小堆实现topk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 package com.itheima.busi; import java.util.Arrays; public class Topk { //堆元素下沉,形成最小堆,序号从i开始 static void down(int[] nodes,int i) { //顶点序号遍历,只要到1半即可,时间复杂度为O(log2n) while ( i << 1 < nodes.length){ //左子,为何左移1位?回顾一下二叉树序号 int left = i<<1; //右子,左+1即可 int right = left+1; //标记,指向 本节点,左、右子节点里最小的,一开始取i自己 int flag = i; //判断左子是否小于本节点 if (nodes[left] < nodes[i]){ flag = left; } //判断右子 if (right < nodes.length && nodes[flag] > nodes[right]){ flag = right; } //两者中最小的与本节点不相等,则交换 if (flag != i){ int temp = nodes[i]; nodes[i] = nodes[flag]; nodes[flag] = temp; i = flag; }else { //否则相等,堆排序完成,退出循环即可 break; } } } public static void main(String[] args) { //原始数据 int[] src={3,6,2,7,4,8,1,9,2,5}; //要取几个 int k = 5; //堆,为啥是k+1?请注意,最小堆的0是无用的,序号从1开始 int[] nodes = new int[k+1]; //取前k个数,注意这里只是个二叉树,还不满足最小堆的要求 for (int i = 0; i < k; i++) { nodes[i+1]=src[i]; } System.out.println("before:"+Arrays.toString(nodes)); //从最底的子树开始,堆顶下沉 //这里才真正的形成最小堆 for (int i = k>>1; i >= 1; i--) { down(nodes,i); } System.out.println("create:"+Arrays.toString(nodes)); //把余下的n-k个数,放到堆顶,依次下沉,topk堆算法的开始 for (int i = src.length - k;i<src.length;i++){ if (nodes[1] < src[i]){ nodes[1] = src[i]; down(nodes,1); } } System.out.println("topk:"+Arrays.toString(nodes)); } }
9.2.4 结果分析